Measuring the Resistance of the Serpinski Gasket

HandsOn 32 - Measuring the Resistance of the Sierpinski Gasket

In the following experiment, you will assemble a fractal resistor network that has the structure of the Sierpinski gasket. In order to assemble a large gasket, this experiment requires cooperation among many collaborators or class participants.

In a classroom setting, each student is provided with nine identical resistors (e.g., 1 kW is fine) and a 5 cm x; 5 cm circuit board (insulating fiberboard with holes punched in it) on which to mount the resistors. Each student group should be provided with an ohmmeter to measure electrical resistance.

Figure 8.7: Construction of the Sierpinski Gasket resistor network following the generation process of Figure 8.1. Here the first generation is shown. Each step in the construction-shown on the following two figures-uses three structures identical to that of the previous step. The same kind of steps are repeated indefinitely to create a "true'' mathematical fractal.

Figure 8.8: The first generation is repeated 3 times to create a second generation gasket with 9 resistors.

Figure 8.9: The second generation is repeated 3 times to create a third generation gasket with 27 resistors.

Figure 8.10: The fourth generation of the gasket with 81 resistors.

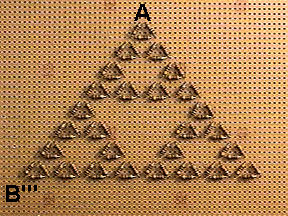The steps in this experiment for groups of three students are:

1. Each student of each team should assemble a 3-resistor gasket (a first generation Sierpinski gasket) as shown in Figure 8.7, then measure the resistance between points A and B. Record this resistance. Then each student should continue, assembling a 9 resistor second generation gasket as shown in Figure 8.8, measure the resistance between points A and B', and record this resistance.

2. Each team of students should construct the circuit in Figure 8.9 by linking together the three circuits they made in Step 1. Measure the resistance between points A and B^'', and record this value. All teams should now compare resistance measurements to be sure that none of the assembled circuits are defective.

3. Three teams should join their circuits together to build the next generation of the gasket shown in Figure 8.10. Measure the resistance between the outer vertices A and B^''', and record the value.

4. If the class is large enough (27 students), the process can be repeated one more time to produce another generation of the gasket. Again the resistance should be measured between the external vertices, and recorded. (If the class is smaller than 27, perhaps some students can build extra circuits.)

5. To analyze the data, plot on log-log paper the measured resistance from vertex to vertex along the vertical axis vs. the number of resistors along one side of the network (i.e., the vertex-to-vertex distance) along the horizontal axis. Draw the best straight line you can through these graphed points.

Q8.14: What would the slope be if you plotted on log-log paper the resistance of a one-dimensional chain of resistors as a function of the number of resistors? What would the slope be if you plotted on log-log paper the resistance of a series of conducting squares of different sizes as a function of the length L of their edges? And for a cube?

Q8.15: The slope you obtained in step 5 is a measure of the dependence of the electrical resistance on the size of the Sierpinski gasket circuit. Does the value you find make sense in relation to the resistance of objects of dimensions 1, 2 and 3 shown in Figure 8.6?

Previous: HandsOn 31 - Resistance of a Fractal Network

Next: HandsOn 33 - Computing the Resistance of the Sierpinski Gasket