HandsOn 31 - Resistance on a Fractal Network

Recall how one calculates the net resistance of two resistors in series or in parallel. We offer two different ways to think of resistance: one is electrical resistance, the other is resistance to the flow of water through pipes.

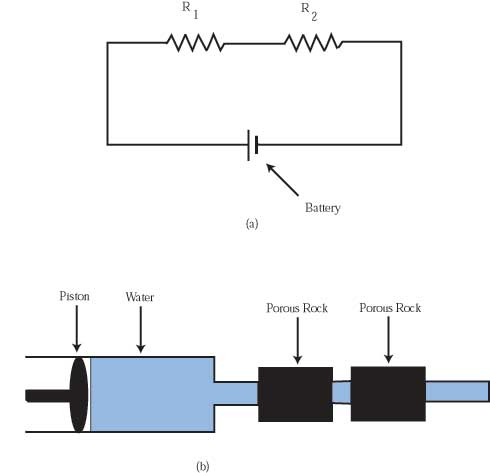
In Figure 8.4(a), two resistors are in series in a circuit with a battery. Resistors literally resist the flow of current. When one resistor follows another, the total resistance of the circuit is R₁ + R₂.

Figure 8.4(b) shows a piston applying pressure to drive water through two porous rocks connected in series with pipes between them. If a constant force is applied to the piston, then the rate of flow of water through the porous rocks is determined by their resistances. Since the two rocks are in a row, the resistances of the two porous rocks are added together.

What is important about series resistances is that they add. If you double the length of a resistor, its resistance doubles. To describe how resistors add in series, we could say that the resistance increases with the total length of the resistors. So, for resistors in series, the total resistance is proportional to length, L, i.e., R L.

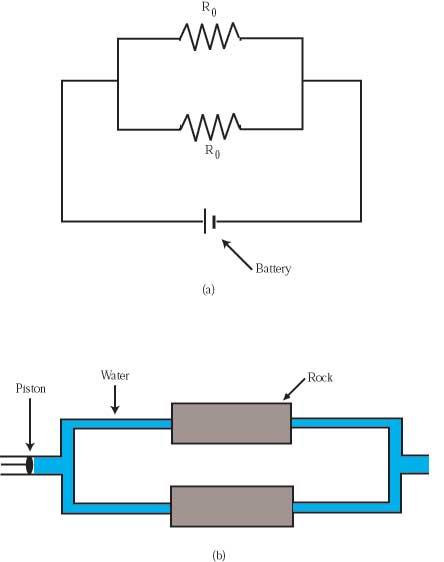By contrast, Figures 8.5(a) and 8.5(b), show two resistors and two porous rocks in parallel. The piston applies the same force to each of the porous rocks. Each rock experiences the same water force as it would if it were alone, with no parallel rock alongside it. Each rock permits the passage of as much water as if it were alone. Taken together then, the two rocks pass twice as much water as either rock alone.

Twice as much water for the same force on the piston means that the two rocks in parallel have half the resistance to water flow as one rock alone. What is important is that the total resistance decreases as more resistors are placed in parallel. If two equal resistors are placed in parallel, their combined resistance is half of the resistance of either one alone.

We could also reason that placing resistors in parallel is equivalent to increasing the cross-sectional area A through which current can flow. Since the resistance decreases with more resistors in parallel, and hence greater cross-sectional area, we can say that R ¹/_A.

Combining our result for series and parallel resistors, we conclude that for ordinary objects the dependence of resistance R of material of cross-section A and length L is

R = r L A .

(8.8)

Here the constant of proportionality r is called the resistivity. The resistivity r has a different value for different materials. For example, copper and carbon have different values of resistivity.

What does this all have to do with fractal dimension?

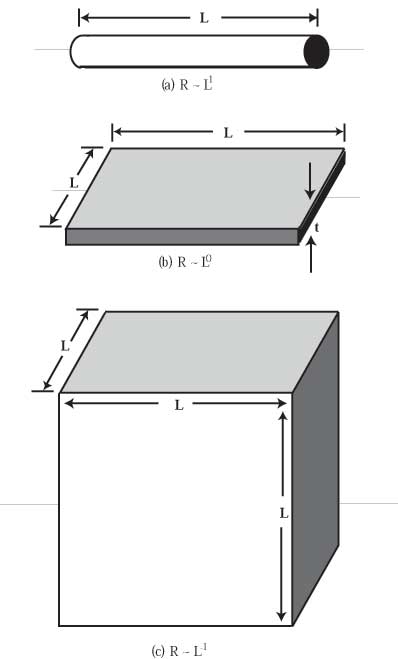
Let's apply the logic of the preceding section to objects with different dimensions, as shown in Figures 8.6(a),(b), and (c). The wire in Figure 8.6(a) is effectively a one-dimensional object, because we vary only its length and not its radius.

Q8.9: Does the actual value of the radius matter in determining whether an object can be considered one-dimensional? Can you imagine cases when it does, and other cases when it does not?

In particular, if we double the length of such a wire, its resistance doubles. From this we conclude that for a one-dimensional object, R L = L¹ (here we emphasize that the exponent is 1).

Now consider the two-dimensional square sheet resistor in Figure 8.6(b). We treat it as two-dimensional because throughout the following we hold its thickness t constant.

Q8.10: When does such a sheet behave like a two-dimensional object, and when is its third dimension important?

The cross-sectional area of the sheet is A = tL. So, if we double its length L and double its width L, then the resistance remains constant since L cancels out in Eq. 8):

R = r L A = r L TL = r t .

(8.9)

The result is that in two dimensions the resistance does not depend on the size of the sheet if we increase both the length and width by the same factor (while keeping the thickness constant). We write this formally as R L⁰. Recall that any quantity to the zero power has the value unity (unity = 1), so in this case R is constant.

Q8.11: Speculate: How is it possible that the resistance is independent of the length and width of the sheet in two-dimensions? Physically what does this mean?

Let's consider the change of resistance of a sheet as we increase its width and length separately. If we double its length in the direction of current flow, then the resistance of the sheet doubles. This action is equivalent to treating the sheet as a one-dimensional object. In terms of water flow through the sheet, we have doubled the distance over which the water must be driven, and hence doubled the resistance to the flow of water.

On the other hand, if we double the width of the sheet in Figure 8.6(b), this is equivalent to adding an identical resistor in parallel. This cuts the resistance in half. Or, in terms of water flow, we have doubled the quantity of water that can flow through when the same force is applied to the piston, which means the resistance to fluid flow has been cut in half.

This combination of series and parallel resistance changes yields the surprising result that in two dimensions, the resistance of a square sheet (of a given thickness) is not dependent on the edge length L of the sheet, but only on the material (that is, on the value of its resistivity r). Equivalently, for flow through a slab of uniform two-dimensional rock, the resistance is not dependent on the width or length of the slab!

Q8.12: Is the above result true only for square two-dimensional sheets? If you double both the width and the length of a rectangular sheet, does the resistance remain the same?

Finally, let's consider the resistance of a three-dimensional cube as in Figure 8.6(c). If we double the cube's length in the direction of fluid or electric flow (making it no longer a cube but something called "a rectangular parallelepiped''), this doubles its resistance. If we double its width (equivalent to putting two of the new parallelepipeds in parallel), we halve its resistance. Finally, if we double the height of the cube, equivalent to putting four more parallelepipeds in parallel, we halve the resistance again. The result is a new cube with resistance

2 . 1 2 . 1 2 = 1 2

times the original resistance. From this we conclude that the resistance of a cube varies with the length of a side as R 1/L = L^-1. This also follows directly from Eq. 8, since A = L² results in

R = r L A = r L L2 = r L .

We have found that in one dimension, R L⁺¹, in two dimensions, R L⁰, and in three dimensions, R L^-1.

All of the above results regarding resistance in 1-, 2-, and 3-dimensional objects (with L describing the size of the object), can be summarized by writing

R L2-d.

(8.10)

where d is the dimension of the object. Verify this by substituting d = 1, 2, and 3 into Eq. 10 and comparing the results with the results of the previous analysis.

         

Q8.13: Speculate: Suppose that a mythical hypercube (a cube in four dimensions-don't even try to draw one!) has edge length L, and resistance R0. What would its resistance be, as a multiple of R0, if you doubled the edge length in all four dimensions.

Now we are experts on the how resistance behaves for objects with integer dimensions. We have attempted to understand the behavior of such objects using simple arguments about resistors in series and parallel.

But what about objects which have a more complicated geometry than that described by integer dimensions? What about fractal objects with non-integer dimensions? For example, what is the resistance of the Sierpinski gasket measured between a variety of points on its structure?

  Previous: 8.3 - Diffusion on a Sierpinski Gasket