HandsOn 33 - Computing the Resistance of the Sierpinski Gasket
 |
 |
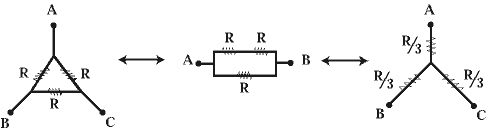
We have made a measurement of the resistance of the Sierpinski gasket resistor network. How can we calculate a number with which to compare it? To compute the resistance of the Sierpinski gasket resistor network in Figures 8.7 to 8.10, we cannot use Eq. 8-there is no direct relationship to cross-sectional area or length. Instead, we use a method for analyzing networks of resistors called the triangle-star method. We apply the triangle-star method to Figure 8.7, as is indicated schematically in Figure 8.11(a).
Begin by analyzing the triangular connection of wires between vertices A, B, and C in Figure 8.11(a). We want to know the value of resistance between vertices A and B. We can redraw this circuit as two series resistors in parallel with the third resistor.
Each of the individual resistors still has a resistance Ro. If you know how to compute the resistance for a parallel resistor circuit, then you can solve this problem mathematically. The resistance between points A and B is 2Ro/3.
You can also arrive at this result by a physical argument. Return to the analogy of pressure being applied to porous rocks. Suppose the current of water through one porous rock is Io. If we apply the same pressure across two such rocks in series, the total current will be Io/2 since the resistance is doubled (Figure 8.4).
Now connect the two ends of a single porous rock across the outer ends of the two porous rocks in series, giving a result that looks like the middle diagram in Figure 8.11. Then apply the same pressure as before between the two ends of this structure (A and B). The same applied pressure forces the same current Io/2 through the branch containing two rocks in series. In addition, a current Io passes through the branch with the single porous rock. The sum of these two flows is 3Io/2. In brief, the same pressure as before causes a greater current (3/2 times as great) through the structure. To achieve this, the equivalent resistance for this circuit of porous rocks must be smaller than that of the single porous rock. How much smaller?
Whether by mathematical formula or physical argument, we come to the conclusion that the resistance between points A and B is 2Ro/3.
The next step of the argument is key: when analyzing a network, the resistors between points A and B, for example, can be replaced by another set of resistors provided the new set of resistors produce the same resistance between these points. For example, in the case of Figure 7.8(a), we can replace the "triangle'' of resistors with a "star'' of resistors each with resistance R0/3. This preserves the resistances between the external points: the resistance between points A and B remains 2R0/3 after the substitution of the new arrangement of resistors. The resistance between point A and C also remains 2R0/3 after the substitution.
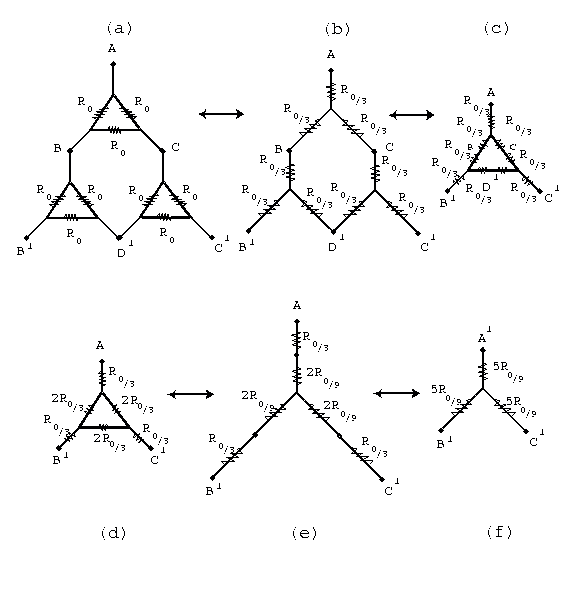
Having simplified the network in Figure 8.7, we apply this result to higher generations of the gasket. The triangle-star rearrangement of the circuit in Figure 8.11 is shown in Figure 8.12, which has five steps. The first step is to replace the three triangles of Figure 8.12(a) by stars in the same fashion as in Figure 8.11. The result yields one large internal triangle in step (c) of Figure 8.12. This in turn can be replaced by a star, again using the method of Figure 8.11. Proceeding in this fashion, we reduce any gasket of resistors to one equivalent star of known resistance. The results for the resistance between the external vertices for gaskets of increasing generation number are:
10R0/9 for the first step gasket (9 resistors) as in Figures
8.8 and 8.12;
50R0/27 for the second step gasket (27 resistors) shown in Figure
8.9;
250R0/81 for the third step (81 resistors) shown in Figure 8.10;
1250R0/243 for the fourth step (243 resistors);
6250R0/729 for the fifth step (729 resistors).
Generally for
the nth step (3(n+1) resistors) the resistance between two external
vertices is:
|
(8.11) |
This is the general formula for the resistance expressed as a function of the transformation step number. But the basic question remains: if you pick up a gasket of length L, and then another of length L', what is the relationship between the two resistances?
What
we are after is a relationship between the resistance and the size;
here size is measured by the vertex-to-vertex length of the gasket.
To derive this relationship, we postulate that as a function
of the vertex-to-vertex distance L the resistance between vertices
can be written as
|
(8.12) |
Having
made this postulate, we test if it is valid. Compare the resistance
for the original single triangle, (2/3)R0 (Figure 8.11),
with that of the first-step triangle, (10/9)R0 (Figure
8.12). See that
|
(8.13) |
|
(8.14) |
|
(8.15) |
|
This method of star-triangle transformation to analyze the Sierpinski gasket
can be generalized to analyze an arbitrary random network on a square or
triangular grid. The power of this method is not restricted to this one
example.
Previous: HandsOn 32 - Measuring the Resistance of the Sierpinski Gasket