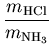HandsOn
23 - Deriving the Motion of Molecules
In the following
exercise you derive the speed of gas molecules and the distance between collisions,
two values that were previously given to you. To do this, you may need to review
a little Newtonian mechanics and thermodynamics.
1. Speed of gas molecules. The average kinetic energy of a molecule in
a gas at absolute temperature T is approximately (3/2)kT, where k is Boltzmann's
constant (1.381 x 10-23 joules/degree Kelvin), i.e.,
From this, find
an expression for the average speed vavg of a gas molecule at room
temperature (approximately 300 Kelvin).
|
Q6.11: Using this expression, first write an expression for vavg.
Using this new expression and the mass of an ammonia molecule, 17 .1.66.10-27kg,
find the value of vavg. |
|
2. Distance between collisions. A gas molecule will experience a collision
if the distance from its center to another molecule is equal to the sum of
their two radii, or approximately equal to the diameter d of a single
molecule. We can think of a moving molecule as sweeping out a volume in one
second which is equal to its velocity v (meters/second) times the area A =
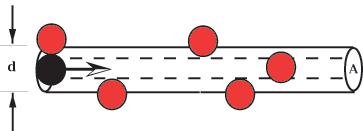
A = 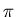 d2, where d is this diameter (see Figure 6.5);
d2, where d is this diameter (see Figure 6.5);
|
| |
volume
second
|
= v
A = 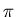 d2. d2. |
|
(6.3) |
|
Figure 6.5: A moving
molecule collides with any other molecule whose center lies within a cylinder
of radius equal to the twice the radius of the molecules.
The moving molecule will collide with any other molecule whose center lies in
this volume. (Of course whenever the molecule hits another molecule, it changes
direction. So the cylinder shown in the figure will be broken up into many short
segments. But the volume swept out will still be given approximately by the
expression above.)
How many gas molecules are to be found with their centers inside this volume
V, on the average? Let the density of gas molecules be n (molecules/meters3).
Then the average number of molecules whose centers are to be found in this
volume is nV. But the volume V is swept out by the incident particle in one
second. Therefore the average number of collisions per second is given by
the expression
|
|
(collisions/second) = |
NV
second
|
= nvavg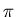 d2. d2. |
|
|
(6.4) |
|
|
Q6.12: From this result and the average speed of the molecule, find
an approximate value for the distance Lstep the ammonia
molecule travels between collisions. To get n, assuming atmospheric
pressure and a temperature of 300 Kelvin, use the gas law equation
n = P/kT, which gives approximately 2.4 x 1025 molecules/m3.
Finally, for ammonia, the so-called collision diameter d is equal
to 3.05 x 10-10m. |
|
|
Q6.13: The values for vavg and Lstep you derived
here may be different from the values you used to estimate the time
t for the ammonia smell to cross the x = 10 centimeter distance. Recalculate
the time t using your new values. |
|
Where along the tube will the dust disk appear? It does not appear in
the center. Why? Because the ammonia molecules move faster, on the average,
than the hydrogen chloride molecules. To see why this is, we need again a little
bit of thermodynamics as well as mechanics. The diffusion tube and its contents
are at room temperature. This means that the kinetic energies of the ammonia
molecules and the hydrogen chloride molecules are, on average, the same. The
kinetic energy K of a molecule is given by the expression
where m is the mass
of the molecule and v is its velocity. Since the two gases are at the same temperature,
the average kinetic energies of their molecules are equal
| |
1
2
|
mHClvHCl2
= |
1
2
|
mNH3vNH32. |
|
(6.6) |
From this we conclude
that the ratio of velocities is
Suppose (wrongly!)
that the ammonia and hydrogen chloride molecules are fired like rifle bullets
from opposite ends of the tube. This corresponds to the "ballistic'' setting
in the Diffusion Chamber program. Then the distance traveled by each in
the time t for them to meet would be given by the expressions
xNH3
= vNH3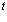 |
|
(6.8) |
and
xHCl
= vHCl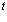 . . |
|
(6.9) |
The ratio of these
positions is therefore
Now, the ammonia and
hydrogen chloride molecules are definitely not fired like rifle bullets
from opposite ends of the tube. Instead, these molecules follow a random walk,
colliding with air molecules as they diffuse along the tube. Evidence
for this conclusion comes from the time required for the powder disk of ammonium
chloride to form. The disk would form in a small fraction of a second if the molecules
traveled directly. Instead, the time required is many seconds.
In many textbooks,
Eq. (10) is used to describe diffusion, even though molecules do not move
ballistically-in straight lines-during the diffusion process. These "derivations''
are wrong. However, it sometimes happens in science that a wrong derivation
can lead to a correct result. In the present case, Eq. (10) turns out to
be correct. This equation is derived form the random walk in HandsOn
25. We will use this result in what follows.
The atomic mass
of HCl is 1+35.5 = 36.5 and that of NH3 is 14+3 = 17, approximately
half as much. Substituting these values into Eq. (10), we have
According to this
theory, then, the ratio of the distances between the powder disk and the ends
of the diffusion unit are approximately 1.5 to one. More careful theory-and
experiment-give a smaller value than 1.46. There are several reasons for this.
One is that HCl (molecular weight 36.5) has more mass than air molecules O2
(molecular weight 32) and N2 (molecular weight 28). Therefore HCl is not deflected
randomly in each collision; it tends to shoulder aside the lighter air molecules
and keep going in the same direction as before the collision. Typically more
than one collision is required to randomize its direction of motion. In effect,
the step length L is made greater (because it goes farther before changing direction
significantly). By equation x2avg/L2 = Nsteps, the number of steps is decreased,
so the HCl diffuses faster than expected, relative to the lighter molecule NH3.
|
Q6.14: Which end will the disk be nearer?
|
|
Previous: SimuLab
15 - The Diffusion Chamber Simulation
![]() d2, where d is this diameter (see Figure 6.5);
d2, where d is this diameter (see Figure 6.5);