HandsOn 25 - Location of the Precipitation Point
The
following derivation uses a full complement of mathematics. Its
purpose is to clarify the usual derivations of the location of the
precipitation point in a diffusion tube (found in many chemistry
books, for example) are inexact in their procedure, though correct
in the final outcome.
Normal distribution. The normal or Gaussian
distribution describes the results of a random walk. This is the
distribution observed in Chapter 2. The Gaussian distribution
describes
the probability P(x) that a walker who starts at x
= 0 will be at
position x after taking N steps randomly back and forth
along a
line, each step of average length
Lstep
P(x) = 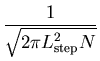 e-x2/(2Lstep2N), e-x2/(2Lstep2N),
|
(6.12) |
In our model of the diffusion chamber, molecules diffuse from the two
ends. We can choose x = 0 for the origin of one molecule, and
x = 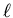 for the origin of the other molecule, where
for the origin of the other molecule, where 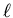 is the length of the
diffusion chamber. Then the probability P1(x)
of finding a molecule
of the first type at position x is
is the length of the
diffusion chamber. Then the probability P1(x)
of finding a molecule
of the first type at position x is
P1(x) = 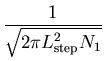 e-x2/(2Lstep2N1), e-x2/(2Lstep2N1),
|
(6.13) |
and, similarly, probability P2(x) of finding a
molecule of the second
type at position x is
P2(x) = 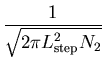 e- ( e- (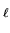 - x)2/(2Lstep2N2). - x)2/(2Lstep2N2).
|
(6.14) |
Here N1 and N2 are the number of
steps taken by the different
kinds of molecules in the same time, and we assume that the average
length
Lstep of one step is the same
for both
kinds of molecules.
There is precipitation of solid (dust) when two molecules of different
kinds meet one another and react. The first precipitation occurs when
the first molecules to meet each other, namely in the extreme
tails of the two distributions.
Hence, the probability of ``meeting the tails'' of the two distributions
would be the product
P1(x) x P2(x),
which would be also the
probability
Ppre(x) of observing
precipitation
at position x
Ppre(x) =
P1(x) x P2(x) =
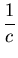 e-x2/(2Lstep2N1)e- ( e-x2/(2Lstep2N1)e- (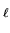 - x)2/(2Lstep2N2), - x)2/(2Lstep2N2),
|
(6.15) |
where the product of the two square roots from (6.13) and
(6.14) is denoted by c (a
constant that does not depend
on x). Next, applying the standard property of the exponential
fraction
eAeB = eA + B,
we can write Eq. (6.15) in the
form
Ppre(x) = 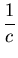 e-
[x2/(2Lstep2N1) + ( e-
[x2/(2Lstep2N1) + (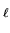 - x)2/(2Lstep2N2)], - x)2/(2Lstep2N2)],
|
(6.16) |
We want to find the position x at which the precipitation is the
most
likely, that is, the peak of the probability given by
Eq. (6.16). It occurs for that
x for which the expression
- [
x2/(2
Lstep2N1) + (
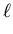
-
x)
2/(2
Lstep2N2)]
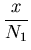 = = 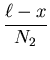 . .
|
(6.17) |
This says that the ratio of distances of the peak from the two ends has
the value:
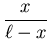 = = 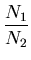 . .
|
(6.18) |
Now we make the argument that for a given average step length, the
number of steps taken is proportional to the average velocity, which is
inversely proportional to the square root of the mass [see
Eq. (6.2)]. Thus the result is:
Hence the initial precipitation occurs at a location whose ratio of
distances from the two ends is inversely proportional to the square root
of the ratio of the masses.
Here we note that the use of distributions (6.13)
and (6.14)
is correct only for the
first precipitation. When
the precipitation has depleted the molecules in the tails of the
distributions, then the distributions are no longer Gaussian. In fact,
it turns out that when a steady state has been reached (when
precipitation removes molecules at the same rate as new molecules leave
the two ends of the diffusion tube), the distributions become straight
lines descending from each end to zero at the point x given by
Eq. 6.19.
|
Previous: HandsOn
24 - Diffusion Chamber
|
![]() for the origin of the other molecule, where
for the origin of the other molecule, where ![]() is the length of the
diffusion chamber. Then the probability P1(x)
of finding a molecule
of the first type at position x is
is the length of the
diffusion chamber. Then the probability P1(x)
of finding a molecule
of the first type at position x is
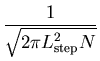 e-x2/(2Lstep2N),
e-x2/(2Lstep2N),
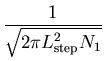 e-x2/(2Lstep2N1),
e-x2/(2Lstep2N1),
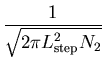 e- (
e- (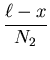 .
.
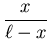 =
=