1. Chamber Length: For diffusion chambers of different lengths, what
are the different times for a "significant number'' of dust particles to
be precipitated? Make a prediction: For a chamber half as long, do you expect
this time to be cut in half? Change the length of the chamber by dragging the
right hand end or by clicking on the Set box at the upper right of the
control panel and entering a number. Record your data and make a graph of the
"diffusion time'' as a function of chamber length. Is the result what you
predicted?
2. Mass Ratio of Molecules: When two molecules of different mass have
the same kinetic energy, the molecule with the larger mass moves more slowly.
Here is the reason: At a given common temperature, all molecules in a gas
have the same average kinetic energy (mv2/2), so one would
expect the molecules with larger mass m to move slower, on the average. Perhaps
slower-moving more massive molecules will diffuse more slowly than less massive
molecules. Therefore, perhaps the initial precipitation disk will not occur
in the middle of the tube. Is this true?
In the diffusion
chamber demonstration, HCl has a molecular weight (atomic mass) of 1 + 35.5
= 36.5, while NH3 has a molecular weight of 14 + 3 = 17, about
half as much. As a result of this difference, which molecule do you expect
to diffuse faster. Do you expect the initial precipitation disk to form nearer
the end of the chamber from which HCl is diffusing, or nearer the end from
which NH3 is diffusing? How much nearer? Write down your predictions.
Test your predictions
with the Diffusion Chamber program. You can try two different mass
ratios in the two panels at the same time, determining the location of the
initial precipitation "disk" in each case.
Do you obtain
more accurate results with molecules of smaller size? Note: The "Length''
of the chamber is measured in the number of horizontal positions that can
be occupied by the diffusing molecules. When you choose a smaller size for
the molecules, more of them can line up from right to left in a given chamber.
In this case, the number displayed for the "Length'' is larger
for a chamber that shows the same size on the screen.
3. Motion of Particles: Our simplest model forces the molecules to
execute a random walk on one dimension-each one moving back and forth along
a line. What is different if the molecules can move in two dimensions, executing
the so-called "2-D random walk''? Will it take longer for the initial
precipitation disk to form? Will this disk appear in a different place? Write
down your predictions, then test them by changing the Motion of Particles
setting to 2-D Random. Write down your results and compare them with
your predictions.
A third way
that particles might move is ballistic. This means constant velocity
in a straight line along the length of the tube. What do you expect to happen
in this case? Will formation of the precipitation disk occur more quickly
or more slowly than for a random walk? Will ballistic motion change the location
of the initial precipitation disk? Write down your predictions.
Try the Ballistic
setting for Motion of Particles and compare the results with your predictions.
Predict what will happen if you carry out the ballistic experiment with the
Infinite Particles setting, then the No new particles setting.
Compare the results with your predictions.
Discussion
- What to Expect
Before going
on to a laboratory experiment with diffusion chambers made of small tubes,
we try to estimate numerical values for some of the results to expect in such
experiments. To simplify the analysis, we return to the one-dimensional random
walk model for diffusion.
From the ManyWalkers
program (SimuLab 3.5) we know that in a one-dimensional
random walk the average of the square of distance traveled is proportional
to the number of steps. Let
Let
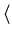 x2
x2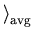 stand
for this average square, let N be the number of steps, and let
Lstep be the average length of
each step, the
average distance between collisions. Then the result can be written as:
stand
for this average square, let N be the number of steps, and let
Lstep be the average length of
each step, the
average distance between collisions. Then the result can be written as:
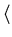 x2 x2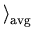 =
NLstep2. =
NLstep2.
|
(6.1) |
Why
Lstep2? This must be
entered in the
equation as a square to make the units correct, since N here has
no
units.
Why Lstep2?
This must be entered in the equation as a square to make the units correct,
since Lstep here has no units.
Notice that
for uniform "ballistic'' motion in a straight line, the formula would
be N = x/L (without the squares).
|
Q6.5: How many steps N will the ammonia molecule take to be detected
a distance x away? To begin to answer this question we need
to know the speed of the molecules at room temperature and the average
distance that a molecule moves between collisions. Here are approximate
values for these two quantities. Later you will derive your own
values for these quantities. |
|
1. Speed of gas molecules. A gas molecule at room temperature moves with an
average speed approximately equal to that of a rifle bullet, about 600 meters/second.
Why doesn't this hurt? This speed is approximately 2200 kilometers/hour (or
1300 miles/hour). Why don't you feel a 2200 kilometer/hour wind all the time?
2. Distance between collisions. A gas molecule in the air travels a distance
between collisions (the length of one step) approximately equal to Lstep
= 1000 x 3 x 10-10meters = 3 x 10-7 meters.
How does this distance compare with the diameter of one hair on your head?
This distance is equal to how many times the diameter of an atom?
From these quantities
and earlier equations, answer the following questions:
|
Q6.6: Suppose that the molecule travels in a straight line, taking
steps only in the forward direction. How many steps N would
it take for the molecule to travel x = 10 centimeters?
|
|
|
Q6.7: In contrast, suppose that the molecule travels in a one-dimensional
random walk. How many steps (collisions) N will it take to
travel x = 10 centimeters?
|
|
|
Q6.8: Let the time tstep represent the average
time that elapses between collisions. Find an expression for tstep
as a function of the particle's average velocity and the average
distance traveled in each step. |
|
|
Q6.9: Therefore how many seconds t are required for the molecule
to move 10 centimeters, on the average, in a one-dimensional
random walk? Express your answer in an everyday unit, such as hours
or days or years. |
|
|
Q6.10: What if the total distance traveled is one centimeter instead
of 10 centimeters. How long is required, on the average, for the
molecule to cover a distance of one centimeter.
|
|
![]() x2
x2![]() stand
for this average square, let N be the number of steps, and let
Lstep be the average length of
each step, the
average distance between collisions. Then the result can be written as:
Why
Lstep2? This must be
entered in the
equation as a square to make the units correct, since N here has
no
units.
Why Lstep2?
This must be entered in the equation as a square to make the units correct,
since Lstep here has no units.
stand
for this average square, let N be the number of steps, and let
Lstep be the average length of
each step, the
average distance between collisions. Then the result can be written as:
Why
Lstep2? This must be
entered in the
equation as a square to make the units correct, since N here has
no
units.
Why Lstep2?
This must be entered in the equation as a square to make the units correct,
since Lstep here has no units.