En muchas reacciones químicas se libera gas o estas ocurren totalmente en el estado gaseoso. La medición de los parámetros del gas, tales cómo el volumen y la temperatura, dan información acerca de la estequiometría de la reacción y de los cambios de energía que se producen en la reacción. Los parámetros del gas son: densidad, presión, volumen y temperatura. Estos parámetros a veces no cambian independientemente entre sí, ellos están relacionados entre sí a través de ciertas relaciones que se llaman leyes de los gases. La idea de que los gases están constituidos por un gran número de pequeñas partículas moviéndose al azar en todas las posibles direcciones da una explicación moderna para las leyes de los gases y es el fundamento de la Teoría Cinética Molecular.

El concepto de Presión

La materia existe en tres estados: sólido, líquido y gaseoso. Todos los sólidos preservan su forma y volumen. Los líquidos tales como el aceite, el agua y el alcohol son distintos de los sólidos. La diferencia con respecto a los sólidos es que los líquidos toman la forma de sus recipientes, pero preservan su volumen. Si tomas un litro de agua y la arrojas en una caja rectangular, seguirás teniendo el mismo volumen de agua, pero con forma cuadrada. Los gases, sin embargo, se comportan de manera distinta que los sólidos y los líquidos. Un gas no tiene forma ni volumen. Un gas se desparramará uniformemente y llenará el contenedor en el cuál se lo pone. Por ejemplo, si abrís una botella de perfume, el olor se desparramará en toda la habitación. Un ejemplo común de gas es el aire. A pesar de que no podemos verlo, está alrededor nuestro. Para probar que el aire existe basta con acercar la palma de tú mano a tú boca y soplar. Otra manera de ver al gas en acción es inflando un globo. Observe que el globo se llena y adquiere una forma a medida que crece. Después lo podes pinchar para experimentar la sensación del gas desparramándose a tú alrededor.

1. Ponga su pulgar sobre la lanzeta y con tú otra mano empuja el émbolo de la jeringa, como se muestra en la figura (a)

2. Empuje al pistón hacia la posición más baja posible y quite su mano de la manija rápidamente, soltando al pistón.(fig b)

fig. a	fig. b

¿Sentiste alguna resistencia a medida que empujabas el pistón?   Puedes explicar lo que ocurre.

Al retirar la mano ¿qué ocurre?

3. Ahora vamos a comprimir el resorte.
¿Sentiste alguna resistencia a medida que empujabas el resorte?   Puedes explicar lo que ocurre.

4 . Deja que se expanda el resorte.

Al retirar la mano ¿qué ocurre?

Una de las mayores contribuciones al estudio cuantitativo de tales propiedades elásticas del aire la hizo el químico Irlandés Robert Boyle (1627 - 1691) hacia la segunda mitad del siglo 17. El descubrió que aunque lo que está actuando sobre el pistón es una fuerza , el parámetro esencial es la cantidad de fuerza aplicada por unidad de área. Boyle estaba hablando acerca del concepto de presión. Boyle llevó a cabo experimentos cuantitativos para medir la relación entre la presión y el volumen de aire.

Presión es el cociente entre la fuerza y el área sobre la cuál ésta fuerza es aplicada.

Una centuria después de que Boyle dedujo su ley, el científico francés Jacques Charles (1746 - 1823) descubrió la existencia de una relación lineal entre la temperatura y el volumen del gas a presión constante. Construyendo un gráfico de la temperatura en función del volumen, descubrió que el volumen de cualquier gas tendía a cero a -273C. No publicó estos resultados. Veinte años después otro químico Francés, Joseph Gay-Lussac, repitió el experimento de Charles, obtuvo los mismos resultados, y los publicó. En ese momento, sin embargo, en el laboratorio uno no podía llegar a temperatura cercanas a -273C , Gay-Lussac sólo pudo demostrar su ley extrapolando en sus gráficos con una línea el volumen hasta cortar el eje de temperatura. Más adelante, a esta temperatura se la llamó cero absoluto.

Joseph Gay-Lussac (1778-1850) continuó investigando a los gases y realizó un experimento a volumen constante. El encontró que, a volumen constante la presión aumenta linealmente con la temperatura. El gráfico de la presión en función de la temperatura es una línea recta. La pendiente de esta línea depende del volumen y del número de partículas de la muestra de gas. Al extrapolar ésta línea, para varios volúmenes, encontró un cruce entre ellas aproximadamente en el punto P = 0, y T = -273C del gráfico. La temperatura de éste punto coincide con la temperatura del gráfico de la ley Charles a presión constante. A ésta temperatura el gas no ejerce ninguna presión. Más adelante, a ésta temperatura se la llamó cero absoluto, y fue entonces que se estableció la nueva escala de temperaturas llamada Kelvin . Cero grados Kelvin, corresponden a -273C. La presión del gas se debe a las colisiones de las partículas contra las paredes, en consecuencia en el cero absoluto las partículas del gas estarían quietas. En términos de la escala Kelvin de temperatura, a la ley Gay-Lussac se la puede expresar como

en donde la constante depende del volumen y del número de partículas de la muestra de gas.

Gay-Lussac, fue uno de los primeros en usar globos aerostáticos con propósitos científicos. Utilizando globos aerostáticos de hidrógeno estudió el contenido químico de la alta atmósfera. En 1804, Gay-Lussac superó la marca alcanzada hasta entonces, llegando a una altitud de 7019 metros. A esta altitud la presión atmosférica es 2.5 veces menor que la del nivel del mar y la temperatura es de -20 C. A pesar de las duras condiciones, Gay-Lussac realizó mediciones muy precisas de las propiedades atmosféricas.


Principio de Avogadro

A principios del siglo 19, la idea de que la materia estuviera constituida por partículas individuales (o sea moléculas, átomos) que pudieran estar o bien moviéndose o en estado estacionario era muy controvertida. El químico Inglés John Dalton (1766-1844), descubrió que en muchas reacciones químicas, las masas de los reactivos y los productos formaban cocientes simples. Concluyó de ésta observación que todos los compuestos químicos están formados por átomos que se recombinan de otra manera cuando ocurre una reacción química.
Esto era una verificación científica sobre la idea de los átomos sugerida por Democritus en el año 400 A.C.
En 1809, Gay-Lussac realizó varios experimentos con gases reactivos demostrando que a presión y temperatura constantes, el volumen no necesariamente se conserva. En otras palabras, si se empieza una reacción con tres volúmenes de un gas, no obtendrá siempre tres volúmenes de gas después de la reacción; la masa se conserva en una reacción química, el volumen no necesariamente. Por ejemplo, si se mezclan dos volúmenes de gas de hidrógeno con un volumen de oxígeno gaseoso a presión constante, el producto de la reacción contendrá dos volúmenes de agua.2

En este ejemplo, el número de átomos (o sea la masa) se conserva, como se puede observar a cada lado de la ecuación.

El científico Italiano Avogadro (1776-1856) explicó los resultados de los experimentos de Gay-Lussac, y concluyó enunciando que en iguales volúmenes de cualquier gas a la misma temperatura y presión hay el mismo número de partículas . El nombre de esta unidad que representa un número fijo de partículas es mol. Un mol contiene el número de Avogadro NA de moléculas, NA=6.02 x 1023. Podemos, entonces, reformular la ley de " Gay-Lussac": a temperatura y presión constantes el volumen de un gas es proporcional al número n de moles

Recordando que las colisiones moleculares con las paredes de un contenedor producen presión, entonces, para una reacción química realizada en un contenedor, a volumen constante, la ley de" Avogadro "dice: a temperatura y volumen constantes la presión es proporcional al número de moles del gas.

Ley de los Gases Ideales

Hasta ahora, hemos estudiado cuatro leyes que describen el comportamiento de los gases. Combinando la ley de Boyle, la de Charles, la de Gay-Lussac, y el Principio de Avogadro, llegamos a la ecuación de estado del gas:

en donde k es la constante de Boltzman y N es el número de partículas en el gas. Usualmente usamos moles en lugar de número de partículas, porque el número de partículas es enorme mientras que el número de moles en una muestra típica de gas en el laboratorio tiene valores más razonables. En un mol de gas hay número de Avogadro NA moléculas. Si el número de moles en la muestra de gas es n, entonces N=n NA es el número de partículas, entonces:

PV=nNAkT

Si definimos R=kNA podemos reescribir la ecuación del gas como:
PV=nRT, en donde R=8.31J/(K·mol) es la llamada constante universal de los gases y n es el número de moles de gas. ésta última ecuación que es la más conocida, es llamada ley de los gases ideales. Las observaciones experimentales de Boyle, Charles y Gay-Lussac sugieren que los gases poseen ciertas propiedades "ideales":

Sin embargo, un gas ideal no es real, sino más bien es una substancia hipotética. Las moléculas de un gas real, en cambio, tienen un pequeño volumen e interactúan entre sí. Por lo tanto existen siempre desviaciones de la Ley de Gases Ideal. Cuando las condiciones se asemejan a las "ideales" (i.e., a bajas presiones y altas temperaturas) las desviaciones son muy pequeñas. A veces las condiciones son "menos que ideales". En estas condiciones, la propiedades de los gases ideales descritas arriba fallan. Por ejemplo, a bajas temperaturas no podemos despreciar las interacciones entre moléculas ya que éstas interacciones son las responsables de las transiciones de fase. Discutiremos estos casos en actividades posteriores.

Consecuencias de la ley de los Gases Ideales

Para chequear la ley de los gases ideales en nuestro "Laboratorio Virtual" obtendremos varias mediciones para diferentes valores del volumen, temperatura, presión, número de partículas y luego vamos a calcular el cociente [ PV/NT]. Si la ley de los gases ideales es válida para nuestro sistema, este cociente debe permanecer constante en un gran rango de los parámetros seleccionados y no deberá depender de la masa de la partícula.

El valor numérico de [ PV/NT] nos dará el valor de la constante de Boltzmann k en nuestras unidades de simulación. En los sistemas reales, usando Joules y Kelvin como unidades k=1.38·10(-23) J/K. En el "Laboratorio Virtual", la constante tendrá un valor diferente ya que estamos usando unidades diferentes.

Basándonos en nuestra discusión acerca de la ley de los gases ideales, sabemos que las partículas de un gas ideal no colisionan entre sí(ya que los gases ideales no tienen volumen no pueden entonces colisionar), mientras que en nuestro sistema colisionan. Primero vamos a chequear la aplicabilidad de la ley de los gases ideales a bajas densidades (i.e., cuando las colisiones son muy pocas). Por otro lado, a bajas temperaturas el sistema condensa y se vuelve un líquido. Usaremos, entonces, temperaturas lo suficientemente altas de manera tal de reproducir el comportamiento de un gas ideal. Después usaremos altas densidades y temperaturas más bajas para observar las desviaciones con respecto al comportamiento ideal y estimar la región de validez de la ley de gases ideales, i.e encontrar las condiciones experimentales en las cuales [ PV/NT] es constante.

Cinética Molecular.

Daniel Bernoulli, el cual ya fue mencionado antes, propuso la idea que las partículas se movían libremente en un volumen sin interactuar unas con otras. Por lo tanto, se mueven a lo largo de líneas rectas a velocidad constante. La presión del gas, entonces, es causada por colisiones de las partículas de gas con las paredes del contenedor, de la misma manera que una pelota de tenis golpea sobre un frontón. Si disminuimos el volumen del contenedor, las partículas del gas tiene menos espacio para moverse, con lo cual colisionan con mayor frecuencia con las paredes, y en consecuencia la presión interna aumenta hasta que iguala a la presión externa. Bernoulli describió el comportamiento molecular y explicó muchos fenómenos propios de los gases. Sigamos sus especulaciones con la ayuda de nuestro Laboratorio Virtual Simulab "Bernoulli". De aquí en adelante nos referiremos a las actividades y cuestiones de este Simulab.
Empezamos con una partícula de gas en un contenedor cúbico de largo L. (Véalo abriendo la pantalla del Simulab para el experimento Bernoulli1 ). La velocidad de la partícula tiene tres componentes: Vx, Vy y Vz. Estas componentes indican cuan rápido se mueve la partícula en cada dirección. La velocidad total es (por el teorema de Pitágoras) . Consideremos por ahora sólo la dirección x. El período de tiempo entre dos sucesivas colisiones es =L/vx. En cada colisión, digamos con la pared IZQUIERDA, la partícula cambia su velocidad de vinic=-vx a vfin=vx. Le lleva tiempos, porque la partícula sale de la pared izquierda y regresa a esta. Esto significa que la aceleración media de la partícula, ax, es

ax= vx -(-vx)

=

2 vx

=

Por lo tanto, usando la ley de Newton F=ma, encontramos que la fuerza media ejercida por la pared sobre la partícula (y por la partícula sobre la pared) es Fx=mvx2/L. Si queremos calcular la fuerza ejercida por las N partículas cuando muchas de ellas tiene distintas velocidades, debemos usar los valores medios:

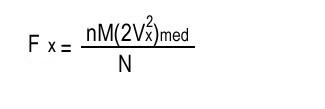
en donde    

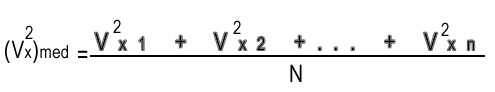
Entonces, la presión promedio es la fuerza media dividida por al área de la pared: P=F/A, por lo tanto

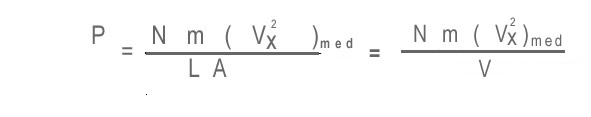
en donde V=LA es el volumen del cubo. Asumimos que todas las partículas se mueven indistintamente en
las tres direcciones, ya que se mueven al azar.

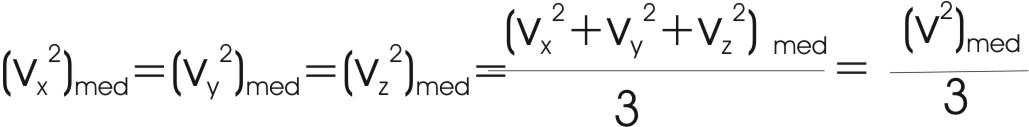
Por lo tanto,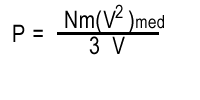

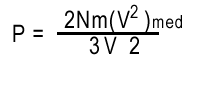En el lado derecho de ésta última ecuación ha aparecido la familiar formula para la energía cinética media. Por lo tanto

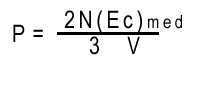
En nuestro SimuLabs el "mundo virtual" tiene sólo dos dimensiones. Por lo tanto, en todas las cuentas en el Simulab , el factor 3 debe ser reemplazado por 2. La presión es igual a la densidad de partículas veces dos tercios de la energía cinética media de las partículas.
Más de 100 años después los científicos relacionaron la energía cinética media de una molécula con la temperatura absoluta del gas. Para un gas monoatómico tridimensional. 3

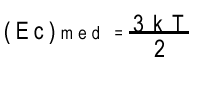en donde k=1.38·10-23J/Kelvin es la constante de Boltzmann. Sustituyendo la última ecuación en la anterior se obtiene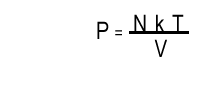

Usando el número de moles n=[ N/(NA)] en vez del número de moléculas e introduciendo la constante universal de los gases R=kNA=8.31 J/mole · Kelvin obtenemos PV=nRT, la cual es exactamente la ley de los gases ideales. La ley de los gases ideales fue originalmente derivada por Clapeyron y Mendeleiev como una generalización de las leyes experimentales de Boyle, Charles, Gay-Lussac y Avogadro. Vemos, entonces que está íntimamente relacionada con la cinética molecular diseñada por Bernoulli.

Ley de Dalton

Hasta ahora, las conjeturas del modelo de gas ideal predicen efectivamente el comportamiento del gas a bajas densidades y altas temperaturas. Trataremos de extender el modelo para poder predecir la presión producida por una mezcla de varias moléculas. Cómo definimos a las moléculas como objetos no interactuantes de volumen cero, cada una de ellas se moverá independientemente en el volumen. Ellas colisionarán con las paredes y producirán presión. Las moléculas de un tipo en particular producirán presión independientemente de la presencia (o ausencia) de otras moléculas. A esto se la llama presión parcial del gas. Las moléculas de otro tipo producirán su propia presión parcial. La presión total en el contenedor será la suma de todas estas presiones parciales. A este enunciado se lo conoce como la Ley Presiones Parciales de Dalton :

P=P1+P2

en donde P es la presión total, y P1 y P2 son las presiones parciales del Gas 1 y Gas 2 respectivamente. Note que cada presión parcial es Pi=RTni/V en donde ni es el número de moles del i-ésimo gas. En nuestro ejemplo i=1,2.

SimuLab: Ley de Dalton
En nuestras simulaciones es más conveniente usar el número de partículas en lugar del número de moles. Además, en las unidades de simulación la constante de Boltzmann es k=1. En consecuencia, las presiones parciales serán Pi=[(Ni)/V]T, en donde N es el número de moléculas de cierto tipo

Referencias

(1) Esto no es verdad en los líquidos, por ej. agua o mercurio; los líquidos no cambian significativamente su volumen cuando están sometidos a presión.

(2) Por supuesto que tendremos que esperar hasta que la temperatura del vapor de agua sea la misma que antes de la reacción.

(3) En dos dimensiones tendríamos (EC)med = [2/2]kT = kT. Nuestros SimuLabs, nuestros "laboratorios virtuales " modelan gases bidimensionales . Además, en unidades de simulaciones k=1, entonces, (EC)med = T.