HandsOn 11 - Ten-Step Random Walk
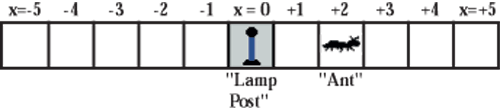
It is easiest to visualize random motion (random walk) along one line, that is, in one dimension. Call x the position of the ant (i.e., walker) on a one-dimensional line. Locate the origin, that is x = 0, at the lamp post. Then let each "step'' of the ant-right or left along the line-be of equal length. One way to picture this is to use one row of a checkerboard or a printout of Figure 3.4.
 |
Choose the direction of the step the ant will take by flipping a penny:
A head or tail is equally likely; therefore it is equally probable that the ant steps right or left.
Do this activity with a partner. Use a silver-colored coin (nickel, dime, or quarter) to represent the position of the ant. To begin, put the "ant'' in a center cell (the position of the lamp post). The ant steps from one cell to the next, right or left randomly, depending on whether the penny comes up heads or tails, respectively.
2. After ten steps, report the final position of the ant, and
whether it is to the right or to the left of the lamp post.
3. Again, the tally keeper puts a big X on a bar graph of the final position
on the blackboard, as you did in HandsOn 10 (Figure
3.2).
|