2.4 - Dimensions and Logarithms
Let's
derive the equations that justify the measurement of the dimension
of an object as the magnitude of the slope of a straight line on
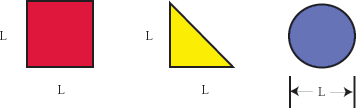
a log-log graph. Think of a pattern that has a fixed area and fixed
overall width L. We are going to cover this pattern with square
boxes of width d and count the number N of the boxes needed to cover
it. For a solid area, we have a dimension of 2 and the general formula
 |
Now we cover any of these shapes with little boxes of width d and area
d2. How many boxes N does it take? The following formula is
approximately correct:
This result is for a 2-dimensional object, such as those shown in Figure
2.10. For a fractal, the dimension is not necessarily 2. Call
the dimension D. Then the corresponding equation becomes:
Take care when measuring the slope D to not use the numbers
along the logarithmic scales. Instead, measure this slope directly, that
is, with an ordinary ruler, as shown in
Figure 2.3, or use the formula:
![]() L
L![]()
![]() = (Const)
= (Const)![]()
![]()
![]() d2,
d2,
![]()
![]()
![]() d2.
d2.
![]()
![]()
![]() = d-2[(Const)L2].
= d-2[(Const)L2].
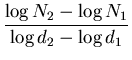 .
.