HandsOn 8 - Creating Your Own Mathematical Fractal
The mathematical fractal coastline we are about to create is called the "Koch curve.'' You will need:
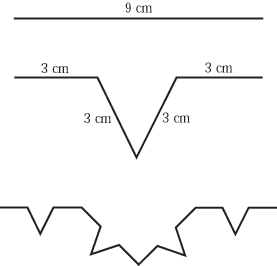
In this procedure, we follow the same rule over and over. The central third of a rubber band segment gets turned into a V, like this:
 |
2. Place thumb tacks into the elastic 3 centimeters from each
end, so that it is divided into 3 equal segments.
3. Take the midpoint of the middle part and pull it perpendicular
to the original line to form a V, with each side of the V being
3 centimeters long. Insert a thumb tack to hold it in place. How
many segments does your coastline have now - that is, how many
straight-line steps does it take to walk exactly along the coastline?
What is its total length now? Complete the second row of your
copy of Table .
4. There are now four segments, each 3 centimeters long. In each
segment, place two thumb tacks so that the segment will be divided
into three 1-centimeter parts; then turn the middle part of each
segment into a V by pulling it perpendicular to the line and inserting
a thumb tack. Each side of each V should be 1 cm. long.
How many straight-line steps does it take now to follow the coastline
exactly? What is its total length? Add this information to your
copy of Table .
5. Now think what the result of the next stage will be. How long
will each segment (step) be? How many steps to follow the coastline
exactly? What is the total length? Add this information to the
copy of Table .
6. Complete the final row of your copy of Table 2.7 by looking at the
pattern of other entries.
| Length of each step | Number of steps to follow coastline | Total length |
| (cm.) | exactly | (cm.) |
| 9 | 1 | 9 |
| 3 | 4 | |
|
|
Plot the table entries on a copy of the log-log graph paper of Figure 2.2.
(Note: Recall that you can multiply all entries on both axes by 10 or 1/10 to
accommodate the range of numbers to be plotted.) The length of each segment
is plotted along the horizontal axis and the number of steps along the vertical
axis. Is the result a straight line? If so, what is the slope of this line?
The accepted value of the dimension of a Koch curve is 1.26. How does the magnitude
of your measured slope compare with this number?
Previous: 2.3 - Mathematical Fractals