|
The AnthillHow do chemical and biological reactions take place? Atoms and molecules have no legs. They cannot walk around and come together to form new molecules and the fractal patterns that we have been studying. How do they find other particles with which to react? One answer to this question is mixing. Air circulates in a room due to differences in temperature and the stirring as people come and go. But chemical and biological reactions go on even in stillness and in cell structures where physical mixing is small or absent. In such circumstances, atoms and molecules get their legs from diffusion. Diffusion is the spread of atoms and molecules due to their random motion from regions of greater concentration into regions of smaller concentration. Without diffusion, life as we know it would be impossible. Imagine the following scenario: In one corner of a school laboratory, Barry opens a bottle of ammonia. Jennifer, who is sitting in the opposite corner of the classroom, grabs her nose and shouts, ``Barry, close that bottle!'' Barry does so, but Jennifer continues to smell the ammonia, so she sensibly walks out of the laboratory.
How would you describe the motions of the molecules? One model
would be to use random walks. The Anthill applet explores the
territory explored by N diffusing walkers---a phenomenon encountered
everywhere in nature (as in Figure 1).
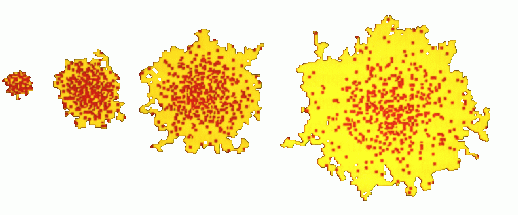
Figure 1: Screen shots of the trajectory of 500 random walkers, started together at the center. Consider a colony of termites let loose from the center of a cell filled with sand. As the termites move, they tunnel through the sand in search of food which is located at the ends of the cell. What can we say about the trails left behind? Another example (see this funny cartoon): A colony of muskrats is found and their locations recorded by an ecologist. As the years go by, the ecologist keeps track of these muskrats and plots contours of the position of the muskrats (as in Figure 2).
Figure 2: Contours of the two-dimensional surface representing the number of distinct sites visited by 500 random walkers. The different colors represent different numbers of steps. What can you say about the roughness of the contour surfaces as a function of time? Check out this other contour plot. Can you think of examples where many particles could be diffusing? HINT: Think of some topics you have looked at in your chemistry, biology, or physics classes. If the ant has unequal probability to move in the four directions, we say that the random walk is biased. For example, suppose the ant has a probability p=1/2 of going north and probability p=1/4 to go west, p=1/4 to go east, and zero probability p=0 of going south. In this case, the walkers never go south and the territory covered moves north quite quickly. Often, nature can be quite biased. Consider the way the smell of an uncorked bottle of ammonia travels from one end of the room to the other. The smell is carried by air currents. In this example, one would have to wait a very long time to smell the ammonia if the molecules were truly diffusing. In a draft, the motion of these ``ammonia particles'' are quite biased.
Now that you've had a chance to experiment, can you answer these questions?
If you want to learn more, check out these cool sites:
This lesson is taken from Fractals in Science. Page was developed by Paul Trunfio and the JAVA applet was written by Gary McGath. Please send comments to trunfio@bu.edu. Copyright 1996-2000, Center for Polymer Studies. |