Simulation of Water

Why Study Water?

Water is an anomolous liquid. In addition, water is ubiquitous, important for everything from protien folding to quenching thirst. Water has a number of unusual properties that cannot that distinguish if from other liquids. For example:

Density Maximum in the liquid state (ie ice floats!)
Growth of Isothermal compressability on cooling (cold water is more "sqeezeable" than warm water)
Formation of Hydrogen bond networks (as shown in picture)

The hydrogen bond network is believed to be responsible for the anamolous behaviour of water. In order to explain the strange behavior of water, people have started to look in the supercooled (liquid below the freezing point) and stretched (negative pressure) regions for answers. It appears that many of the anomalous properties can be explained by the behavior at supercooled temperatures, including the possiblity of a second low temperature critical point. At temperatures below this possible critical point, there exist TWO liquid phases, one high-density and one low-density (strong bond network). This is analogous to cooling steam below the high temperature critical point where a high density fluid (liquid water) and a low density fluid (water vapor) condense out. 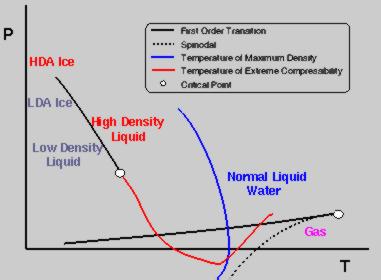[See phase diagram]. Here is a short movie showing the cavitation of an 8000 molecule system (I also have a version with music - if you have agood connection). This pressure is below the spinodal shown in the phase diagram.

Why Simulate Water?

When water is cooled below the freezing point, it naturally tends to nucleate to form ice. This is in large part due to inhomogenities in the liquid that provide a nucleation site. Thus, to study deeply supercooled water, people have turned to simulations. Simulations also allow one to simulate strecthed states, which are difficult to obtain experimentally. Click here to try out a water simulation you can run over the web!

Fast Multipole Methods?

The Coulomb force is responsible for hydrogen bonding in water, and is a long range force. Therefore we cannot employ simple cutoff methods used in Lennard-Jones type systems. This leaves us with an order N^2 problem, a very large computational overhead. These methods have been used successfully in the past, but are limited so system of size (roughly) 216 particles. Naturally it is hard to pick out bond networks for a cube of 6 molecules per side.

Fast Multipole Methods are used becuase they reduce the problem to order N. This is achieved by breaking space up into a heirarchial tree. For cells in the tree that are well-separated, we can compute the electrostatic interactions via a multipole expansion. This reduces the calculations a tremendous amount without losing significant accuracy. For more of fast multipole methods, see the refernece section.