As you saw in Sect .2.3 from the studies of the polymers they collapse in dense globule as the temperature decreases. This collapse is characterized by a steep but not infinite slope of the potential energy vs. temperature.This behavior is characteristic of the fluid near its critical point where no distinct phases exist. The globule is amorphous and its shape changes all the time. Proteins although they also collapse at low temperature into a dense globule and unfold at high temperature they do it in a quite different way. The main difference is that the protein globule always has the same structure which is called `native structure'. Beeing in this structure allows protein to act like a nanoscale robot which binds to other specific targets such as small molecules ligands, other proteins and DNA. For example hemoglobin binds to O2 and C O2. Other special protein topoizomerazes which can cut DNA and glue them back together in order to distentangle DNA strand in mitosis. Miosine acts like micromotor sliding along acting chains during muscle contraction. All this amazing properties are possible because protein, a string of different aminoacids, somehow folds itself into native state. Imagine a shoelace which can tangle into a knot and disentangle by itself without human intervention! Scientists have discover that Aminoacid sequence completely determine the native structure. Some Aminoacids are hydropholic and attract to each other. Other are hydrophilic, they attract to surrounding water. The main problem of the protein science is, given the chemical sequence of protein, to determine its three dimensional shape in the native structure. Or viceversa, knowing the three dimensional shape, design the chemical sequence that would fold into it. There is an entire spectrum of different repulsive and attractive properties of aminoacid which in our simple universe could be encoded by 3 20 x 20 matrices of rAB, RAB and eAB where A and B stand for different aminoacids. This would allow to design powerful drugs and there are many scientific groups around the globe that competes wich each other to do it first. So fare nobody fully succeed in it, however the first insights are already obtained, and there is a hope that someday a powerful computer, given the potentials of interaction between different aminoacids, would be able to predict native structures and design proteins for specific tastes. Our program Universal, made in collaboration with the group of Prof. Shaknovich in Harvard University, represents the first steps in this direction. The main drawback of our program is that the aminoacids are presented by structureless balls, this allows us to do simulations much faster than other groups who represents the aminoacids by all atoms interacting with each other with realistic interatomic potentials. Instead of specifying complex potentials between aminoacids, we take the known native state of small protein CHR3 domaim which consists of 57 aminoacids and postulate that aminoacids who are between 75 A0 of distance in the native state attract each other while the others who are further away repulse. This give us a 57 x 57 matrix of rAB, RAB and eAB. The protein designed like this unfolds at high temperature and fold into the perfect native state at low temperature. Of course this is not the full solution of the protein folding problem (which would be if we use only 20 x 20 matrices and do not directly use the structure of native state) but a significant step in this direction. Several scientific papers have being published and submitted to important journals by our graduate students J. Borreguero, F. Ding and postdoctoral research associate N. V. Dokholyan. Thus experimenting with our simulab of protein folding you will do the cutting the edge research.
|
| time | temperature | Potential Energy | Total energy |
| 1000 | |||
| 2000 | |||
| 3000 | |||
| 4000 | |||
| 5000 | |||
| 6000 | |||
| 7000 | |||
| 8000 | |||
| 9000 | |||
| 10000 | |||
| 11000 | |||
| 12000 | |||
| 13000 | |||
| 14000 | |||
| 15000 | |||
| 16000 | |||
| 17000 | |||
| 18000 | |||
| 19000 | |||
| 20000 |
1. Open Universal Application. Press on Play Movie and select folding.mov
Press Forward.
~ You see a fully unfolded protein at the temperature above the folding transition.
We take away the heat from the protein so that the total energy steadily and
slowly goes down. Watch the dancing in the unfolded state. The protein dances
almost like a snake.
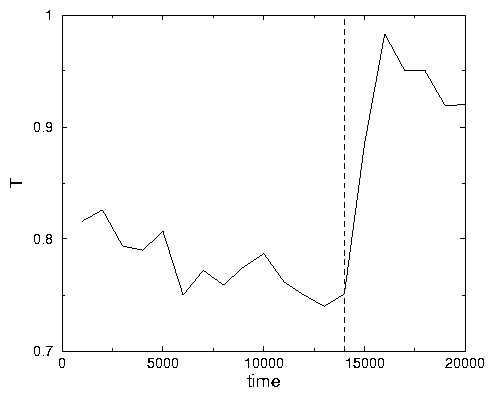
~ Watch the graphs of temperature and potential energy. They are widely oscillating
due to the protein dance. When protein unfolds the potential energy goes up
while the kinetic energy goes down (the temperature in this simulation is
defined like 2/3 of the average kinetic energy per aminoacid).
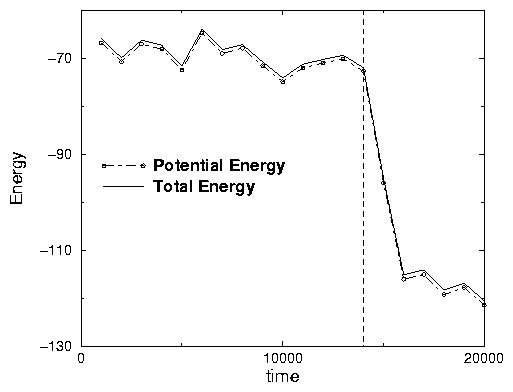
~ Watch the graphs of Total Energy it is steadly decreasing (See Fig .2.8).
Note that protein already form some secondary structures such as the sloops
between the purple and violet stretches, called `hairpin'. It almost never
unfolds. At time about 14000 (or 3400 frames) the protein suddenly finds its
native structure and quickly folds. The potential energy dramaticaly goes
down and the temperature goes up (See Fig .2.8).
The latent heat of folding is released similar to the crystallization process.
After folding the protein lives at much higher temperature thatn before. This
means that before the protein was in a supercooled metastable phase, like
liquid in the crystallization before the critical nucleous appears. Thus the
protein foldin resembles the first order phase transition of freezing, when
the potential energy of the two phases that can coexist is dramatically different.
One phase, (disordered) unfolded (or liquid), has high entropy but low energy.
Another phase (ordered) native state (or crystal) has low energy and low entropy.
The free energy F = U - T S of both phases are equal and the system in order to fold (crystallize) must
overcome the free energy barrier with low entropy but high energy. This transitional
state , in the freezing, is characterized by the emerging of the nucleous
(specific arrangement of atoms in the liquid which shifts the equilibrium
towards the crystalline state). This lead protein researchers to the conclusion
that the same happens in the protein folding: specific arrangement of aminoacids
once formed shifts the equilibrium towards the native state. The difference
between liquid and the protein is that in liquid all the atoms are indistinguishable
while in protein all aminoacids are different, identified by their position
in the chain and the chemical nature. Thus the critical nucleus in the protein
involves all the time the same aminoacids. These aminoacids are extremely
important because their mutation may dramatically change the folding properties
of the protein thus lead to alteration of its structure in function.
Graduate student Feng Ding found that in the protein we study the critical nucleus is formed when aminoacids E 16 (yellow) and M48 (violet) come together. Try to notice this moment in the movie.
2. Rewind the movie till beginning. Open the Averaging for Movies window
from the Option menu. After each 1000 time units (200 frames) stopt
the movie, record the data into your table and reset averages. At the end
you will have 20 maesurements.
|
~ Note that these curves ressemble the behavior of the freezing curve near
nucleation with large amount of latent heat released.
A2.30: See Fig .2.8
| time | temperature | Potential Energy | Total energy |
| 1000 | 0.816 | -66.84 | |
| 2000 | 0.826 | -70.78 | |
| 3000 | 0.7937 | -67.09 | |
| 4000 | 0.790 | -68.16 | |
| 5000 | 0.807 | -72.48 | |
| 6000 | 0.750 | -64.76 | |
| 7000 | 0.772 | -69.05 | |
| 8000 | 0.759 | -67.97 | |
| 9000 | 0.775 | -71.61 | |
| 10000 | 0.787 | -74.96 | |
| 11000 | 0.762 | -72.07 | |
| 12000 | 0.750 | -71.05 | |
| 13000 | 0.740 | -70.22 | |
| 14000 | 0.751 | -72.76 | |
| 15000 | 0.885 | -95.98 | |
| 16000 | 0.983 | -116.1 | |
| 17000 | 0.950 | -115.1 | |
| 18000 | 0.950 | -119.3 | |
| 19000 | 0.919 | -117.8 | |
| 20000 | 0.920 | -121.5 |

