SimuLab 2: Freezing and Melting



                        

You will be able to:

a) Study the freezing and melting curve;


b)Find the triple point;


c)Find the equilibrium Gas pressure near Liquid and solid surfaces.





2.2.1  Post-Lab In-Depth Discussion

Latent Heat in phase transitions

As gas start to condense, the latent heat of condensation is released and it has to be taken away, thus only part of the heat that is taken away comes from the kinetic energy of the gas. So the rate of temperature decrease. As almost all the gas condenses, the temperature again start to decrease faster. Once the temperature goes below the freezing point a spontaneous nucleation occurs. At first the nucleus grows fast because the liquid is deeply supercooled (See Sect.2.1.1). The latent heat of crystallization released is so large that the heat bath cannot absorb it at once, so the temperature goes up until the crystallization rate decreases to a value at which the latent heat release rate is equal to the heat exchange rate and the temperature stays constant for a long time until all the liquid crystallizes. Since the heat exchange rate is very small (0.0001) the crystallization is very slow: the liquid and the crystal are almost at equilibrium. As a result a perfect crystal with no defects emerges. Moreover at this temperature the droplet is at equilibrium with the Gas, which as very low density (but still non zero). It means that all three states of matter at this temperature are at equilibrium. Such temperature is called the triple point. Once the liquid crystallizes the release of latent heat stops and the temperature starts to decreases.

Vapor Pressure

The equilibrium pressure of the gas is proportional to the evaporation rate. Indeed the low density gas at equilibrium is well described by the ideal gas law. It's density is proportional to the pressure. On the other hand the number of collisions of gas molecules with liquid per second is proportional to the density of gas. Hence the condensation rate is proportional to the gas pressure and as the evaporation rate at equilibrium is equal to the condensation rate, so it is also proportional to the gas pressure. The evaporation rate is proportional to the probability that the molecule in liquid gain the potential energy H that is the difference between the potential energy on the gaseous phase (0) and in the liquid phase. This can occurs if the molecule gains the kinetic energy of 4 in these case. The kinetic energy of molecules are distributed with Maxwell distribution
p ~ exp(- m v2
2 kB T
 )

. Hence the probability to leave the liquid phase is proportional to
exp( -H
2 kB T
 )

, and thus
P = P0exp- H
kB T
 ,
where P0 is some proportionality coefficient. Taking logaritms of both sides of this equation:
ln (P) = ln(P0)- H
kB T
(2.1)

So if we plot ln(P) as a function of 1 / T the arrhenius plot is a straight line. In our simulation kB = 1 and thus the slope is -H, where H is the potential energy per atom in the liquid.

Answers to the question

Simulab 2

figures/Tvstime.png
Figure 2.3: Temperature as function of time for freezing ° and melting [¯]. The plateau in each case shows the temperature of temperatures of those transition. The dashed-lines are used a guide to show the values of that temperatures in freezing (T = 0.537) and melting (T = 0.546).


A2.15: As the temperature goes down, gas start to condense, it forms a compact droplet surrounded by few molecules. Finally a little crystal appears inside the droplet . At this point the temperature goes up and stays at the plateau as the crystal grows. Once the liquid crystallize the temperature starts to go down again. As the temperature decreases the number of particles in the gaseous phase decreases.



A2.16: The liquid emerges at t = 10000 (100 frames). The crystal at t = 50000 (500 frames) and stops at t = 75000 (750 frames).



A2.17: The temperature goes down because we take away energy from the system, almost at constant rate. At first the rate at which the temperature changes is fast because almost all the heat is taken from the kinetic energy of the Gas See Sect2.2.1.



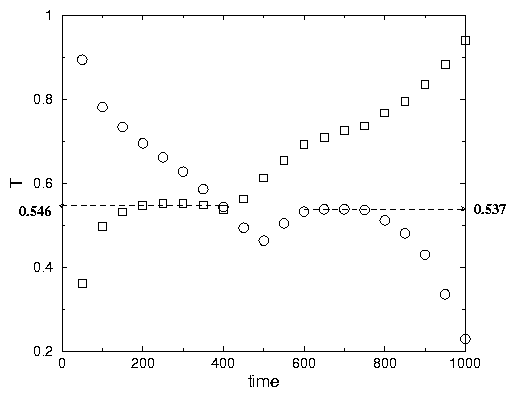
A2.18: The plateau region corresponds to the crystallization temperature. The crystallization temperature is T = 0.537 (See Fig .2.3)



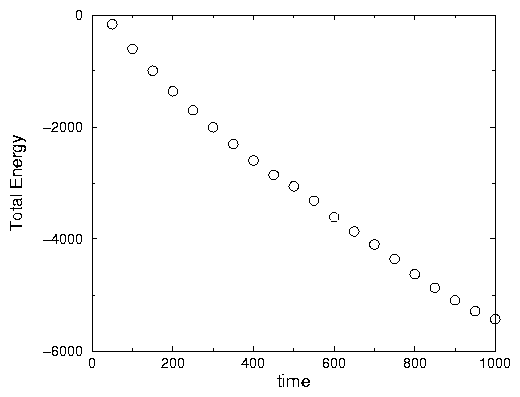
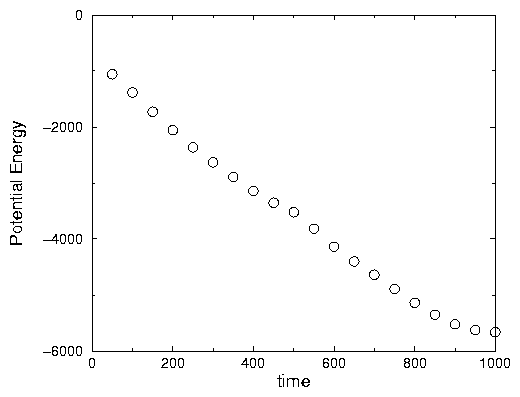
A2.19: Theses graphs are monoatomic since we take out the heat from the system almost at constant rate (See Fig .2.4).

figures/TEvstime.png figures/PEvstime.png
Figure 2.4: Plot of the total and potential energies as function of time during freezing. Theses graphs decrease monoatomic.



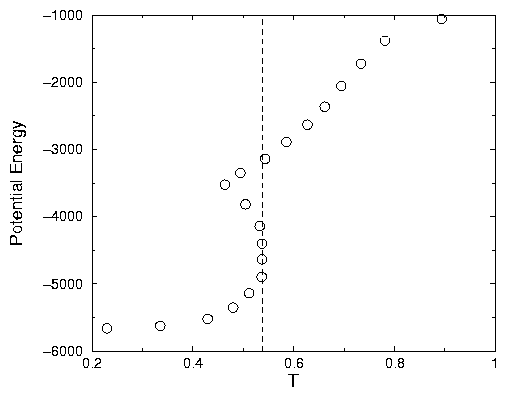
A2.20: In the graph of the potential energy as a function of the temperature we see a region of regular liquid above the critical temperature of crystallization (T = 0.537) (See Fig. 2.5). Below the freezing point the liquid in a supercooled state coexist with the crystal. At the critical point we see a plateau characteristic of a phase transition where liquid and crystal coexist. The height of this plateau is the latent heat of crystallization which value is 1722.

figures/PEvsT.png
Figure 2.5: Potential energy as function of the temperature during the crystallization °. The dashed line is used as a guide to show the transition temperature Tc. The height of the step is the latent heat of crystallization. Notice the region of supercooled liquid in coexistence with the crystal below Tc.



A2.21: The melting temperature is 0.546 and corresponds to the plateau in Fig .2.3 . During freezing it was 0.537. The difference is 0.01. During melting the liquid was growing. The equilibrium was shifted towards the liquid state. The crystal was superheated. Hence the temperature was higher that during freezing when the equilibrium was shifted towars crystalline state and the liquid was supercooled. One can expect that the true equilibrium temperature is somewhere in between and we can assume that it is 0.542 ±0..05 which is also the triple point temperature because the gas is also at equilibrium.


A2.22: During melting the pressure is 1.81 ·10-4. During freezing it is 1.42 ·10-4. The average pressure is the 1.6 ·10-4 ±0.02. Hence the triple points parameters are T = 0.542 ±0.0005 and P = 1.6 ·10-4 ±0.02.


A2.23: See Fig .2.6

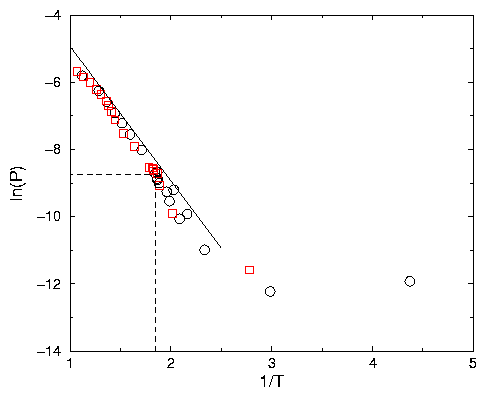
figures/PvsinvT.png
Figure 2.6: Ln plot of pressure vs. 1/T for both process: freezing ° and melting [¯]
. The dashed lines shows the triple point and the solid is used as a guide to show the slope -4. Note that above T = 0.73 both curves coincides.


A2.24: During the fast cooling the condensation rate is higher than the evaporation rate. It means that the density of gas surrounding the liquid is higher than the equilibrium one. During the fast heating the evaporation rate is higher than the condensation rate. It means that the density of gas is lower than the equilibrium one. During cooling, the gas is supercooled or supersatured. During heating the liquid is superheated. The equilibrium pressure must be in between the two curves. Above T = 0.73 the liquid does not exist and both curves coincide.


A2.25: The slope is about -4 See Sect. 2.2.1.


A2.26: The slopes is -6.