Virtual Molecular Dynamics Laboratory:

Bridging the Gap Between the Microscopic and Macroscopic

Center for Polymer Studies

Science and Mathematics Education Center

Boston University

This material is based upon work supported by the National Science Foundation under Grant Nos. MDR-9150079, CDA-9616565, and ESI-9553883. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Virtual Molecular Dynamics Laboratory:

Bridging the Gap Between the Microscopic and Macroscopic

The text includes an accompanying CD-ROM of software (we call SimuLabs) for Windows platform. Macintosh, Unix, and Spanish versions are available via our Web site:

http://polymer.bu.edu/vmdl

Comments and feedback are most appreciated and can be sent by email to:

wamnet@polymer.bu.edu

Overview

Principal Research Scientist:	Sergey Buldyrev
Project Director:	Paul Trunfio
Teacher Developers:	Reen Gibb
	Joseph Jordan
Research Scientists:	Lidia Braunstein
	Sergei Siparov
Programmers:	Amit Bansil
	Anna Umansky
Web Developers:	Tim Blount
Assessment Coordinator:	Mary Shann
Principal Investigator:	H. Eugene Stanley

Our classroom experience and research have revealed a startling discrepancy between the mental models of microscopic processes possessed by students and those possessed by research scientists. In many courses, students are asked to learn about and believe in a macroscopic world without any direct information on which to base the belief. Research scientists, on the other hand, have a mental model in which macroscopic events are understood in terms of the microscopic behavior of a huge number of individual particles.

Our VIRTUAL MOLECULAR DYNAMICS LABORATORY addresses this problem by providing a set of research-based molecular dynamics software tools and project-based curriculum guides. The VIRTUAL LABORATORY enables the student to visualize atomic and molecular motion, manipulate atomic interactions, and quantitatively investigate the resulting macroscopic properties of a range of biological, chemical, and physical systems.

For example, our software package SIMPLE MOLECULAR DYNAMICS (SMD) allows students to manipulate parameters such as pressure, volume, temperature, particle number density, and particle mass. Students are also able to design their own experiments, visualize atoms and their behaviors, and obtain in-depth, quantitative data which they can graph in many different ways. For example, students can copy and tile graphs and discover how various parameters such as potential energy, kinetic energy and total energy versus time relate to one another. Investigations include topics such as: states of matter, enthalpy, Boyle's Law, Charles' Law, Ideal Gas equation, Gay-Lussac's Law, Avogadro's Principle, Dalton's Law, diffusion, Graham's Law, kinetic molecular theory, and Maxwell distribution of velocities. The accompanying SIMPLE MOLECULAR DYNAMICS PLAYER (SMDPlayer) allows students to view and analyze movies they have created themselves of previously-saved simulations.

Accompanying curriculum guides are a collection of project-based " hands-on'' and " simulab'' activities that are meant to enhance existing curricula. The " hands-on'' activities hook the students' interest and focus their attention on the macroscopic phenomena. Then they investigate the underlying atomic dynamics using the " simulab''. Each simulab consists of a brief discussion of the concept to be investigated, learning goals, procedure, questions integrated throughout, and a teacher's guide.

Other applications currently under development include UNIVERSAL MOLECULAR DYNAMICS which allows students to design simulations of simple chemical reactions, build complex chemical compounds such as polymers, and model complex systems such as diffusion chambers, cell membranes, or internal combustion engines. Also under development is the three-dimensional water application, which introduces students to the microscopic dynamics of water by simulating how water properties arise from hydrogen bonds and from the geometry of bonding interactions and the dynamics of the solvation process.

We have recently been awarded a grant from NSF for a series of nationwide teacher training workshops using the VIRTUAL LABORATORY. Beginning in 2001, our workshops will feature annually two 2-week summer institutes, three 3-day regional workshops, and science convention workshops The project's major features are to (1) prepare 336 high school chemistry, biology, and physics teachers to incorporate the VIRTUAL LABORATORY curriculum into their introductory science classrooms, (2) introduce these teachers to the role of mentoring in a cooperative learning classroom environment in which students act as research workers, learning through hands-on activities, laboratory experiments, and visual and interactive computer models of chemical, physical, and biological systems, (3) encourage participating teachers to develop new activities, approaches and lessons utilizing the computer as a simulator, and (4) develop online teacher resources including lesson plans, assessments.

Simple Molecular Dynamics Feature Tour

Chapter 1
Temperature and States of Matter

Sensations of temperature are a part of everyday experiences. My friend's hand is warm. The ice in my drink is cold. Florida in July is hot. When we quantify these sensations by measuring temperature, we usually find: the warmer the sensation the higher the temperature.

We also know from experience that temperature can affect the `state' of matter. Water becomes ice when we put it in the freezer and steam when we boil it on the stove.

The first step towards uncovering the mystery of temperature was made more than two thousand years ago when the ancient Greek philosopher Democritus formulated the hypothesis that all objects are made of invisibly small, constantly moving particles called atoms. It was not until the mid-nineteenth century, that scientists built upon the ancient atomic hypothesis to formulate a model of what the individual atoms or molecules might be doing that could explain temperature and the state of matter.

1.1 States of Matter

Discuss the following questions:

Q1.1: What are the states of matter?

Q1.2: How are ice, liquid water, and steam similar?

Q1.3: How are ice, liquid water, and steam different?

Q1.4: Imagine that you could make a " microscopic'' dive into a pool of water and see the individual water molecules. What do you see happening to the molecules as the water is cooled and ice begins to form?

Q1.5: What would you see as water is heated and begins to vaporize?

BEGIN ACTIVITY

SimuLab 1: Temperature and the State of Matter

Your objective is to:

Recognize the differences between solid, liquid, and gas from the microscopic point of view.
You will be able to:

Describe the phase transition from liquid to solid and from liquid to gas in molecular terms.

Contrast the motion of particles in the solid, liquid and gaseous phase.

Describe a liquid-gas equilibrium.

Describe the relationship between states of matter and temperature.

Q1.6: Describe, in drawings and in words, your conception of the molecular structure of a substance in the solid, liquid, and gas states.

Q1.7: Describe what happens when we heat a solid in terms of particle motions and overall structure?

1. Open SMDPlayer, select IntroStatesofMatter from the StatesofMatter folder. Press Play. Study the captions and follow the instructions. When you are finished, select File - Quit

This is an introductory movie that visualizes the three states of matter at the molecular level and the effect of increasing temperature.

Q1.8: In the introductory movie we saw that as we increase the temperature, solid melts into liquid and liquid evaporates into gas. Describe, in drawings and in words, what would happen as we decrease the temperature of a gas? (Answer such questions as: Do the molecules move faster or slower? Does the gas expand or condense?)

2. Open SMD, select Solid in the States of Matter folder. Press Start. In order to speed the simulation switch Iterations Between Displays to 100.

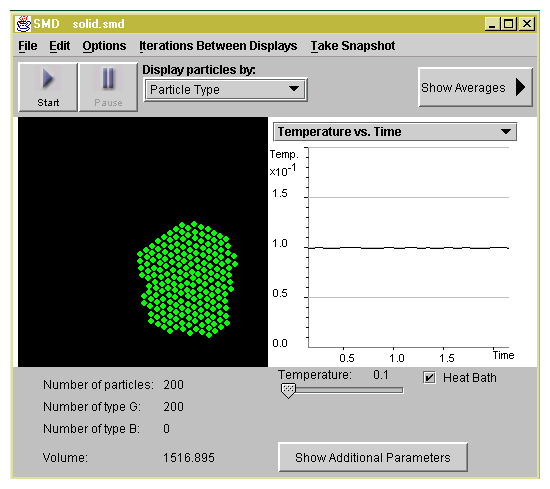
In this experiment you are visualizing 200 particles at the molecular level. The particles are in the solid state at temperature T=0.1 as shown in Figure 1.1. Our program uses computer units for all the parameters. You can see temperature and all the other parameters in real units by selecting Show Averages and then selecting Show Real Units.

figures1/solidc.png

Figure 1.1: You see 200 particles at a temperature far below the freezing point of the substance we are simulating. The horizontal axis of the graph shows the simulation time. The vertical axis shows the temperature of the system. The particles are frozen in a triangular crystal.

3. Select Display Particles by: Trajectories. Wait no more than 10 time units. Pause the simulation. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears type in: " Solid (T=0.1)'' and press Ok.

You are saving a snapshot of the trajectories of particles in the solid state for later comparison. Trajectory is another word for the path a particle travels over time.

Q1.9: Which phrase best describes the trajectories of particles. " The particles appear to be . . .''
(a) fixed in position
(b) slightly wobbling around a fixed position
(c) moving along in curved lines
(d) moving along straight lines

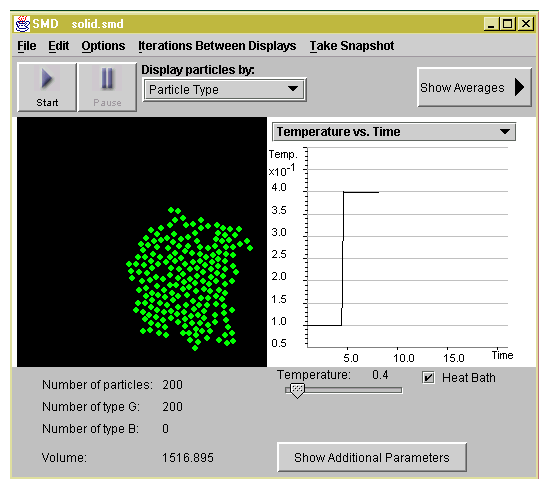
4. Select Display Particles by: Particle Type. Using the scroll-bar increase the Temperature to T = 0.4. Press Start. Wait at least 20 time units for the particles to spread.

As the temperature increases, the regular pattern of the solid is destroyed as shown in Figure 1.2. The molecules begin to move more freely.

figures1/liqc.png

Figure 1.2: Your system undergoes a phase transition from the solid state to the liquid state. The graph shows the change in the temperature that you made in Step 4.

Q1.10: Predict what would happen if you lower the temperature back to T = 0.1. Time permitting, check you prediction. Make sure you then set the temperature back to T = 0.4 and wait again for 20 time units before proceeding to Step 5.

5. Select Display Particles by : Trajectories. Wait no more than 5 time units. Pause the simulation. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears type in: " Liquid (T=0.4)'' and press Ok.

You will compare the trajectories of the particles in the liquid state with trajectories of particles in the solid state.

Q1.11: Describe the differences between your snapshots of trajectories from " Solid (T=.1)'' and " Liquid (T=.4).'' Your descriptions should include a comparison of the particle motion between the two states.

6. Select Edit - Reset Trajectories and press Start. If the trajectories get too cluttered, select again Edit - Reset Trajectories.

Observe that some particles leave the liquid state and move in straight paths. These gas particles sometimes rejoin the liquid state and sometimes leave it. You are visualizing two states of matter at equilibrium.

Q1.12: What real-life examples can you list where a gas and liquid co-exist in the same system?

Q1.13: Which phrase best describes the trajectories of particles in the liquid phase . " The particles appear to be . . .''
(a) fixed in position
(b) slightly wobbling around a fixed position
(c) moving along in curved lines
(d) moving along straight lines

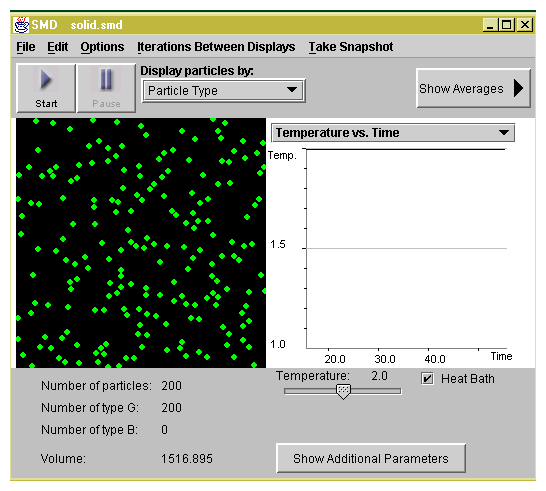
7. Pause the simulation. Switch Display particles by: Particle Type. Using the scroll-bar increase the Temperature to T = 2. Press Start and wait at least 20 time units.

As the temperature is increased, the particles leave the liquid state and become gas as shown in Figure 1.3.

Q1.14: Which phrase best describes what is happening as the particles begin to fill your container. " The particles are . . .''
(a) melting
(b) freezing
(c) evaporating

figures1/gasc.png

Figure 1.3: A snapshot visualizing the gas state.

8. Switch Iterations Between Displays to 5. Switch Display Particles by: to Trajectories. Wait 5 time units. Pause the simulation. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears type in: " Gas (T=2)'' and press Ok.

You will compare the trajectories of the particles in the gas state with trajectories of particles in the solid and liquid states.

Q1.15: What are the differences between the trajectories in the liquid and gas states? Try to explain why the trajectories are different.

Q1.16: Using your snapshot gallery, describe the differences in the three states of matter in terms of particle motion.

Q1.17: Describe in drawings and in words how the state of matter is related to temperature.

9. Switch Iterations between Displays to 100. Select File- Reset Experiment.

You can further investigate the trajectories of individual particles in the three states of matter.

10. Select Edit - Select Particle and choose one particle at the center of the solid. Select Display Particles by: Selected Trajectories and press Start. After 10 time units, Pause the simulation. Raise the Temperature to T = 0.4 and press Start. For approximately 20 time units, observe the changes in the trajectory of your selected particle. Pause the simulation and increase the Temperature to T = 2. Press Start. Watch the trajectory of your chosen particle for another 20 time units. Press Pause.

You are watching the behavior of the chosen particle at different temperatures.

Q1.18: Explain the changes observed in the particle trajectory as the temperature is raised.

11. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears, type " Center''.

You will compare this " center'' particle with a particle from the " edge'' of the solid.

12. File -Reset Experiment. Repeat the step 10 but now select particle from the edge of the solid.

13. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears, type " Edge''.

Q1.19: Compare your snapshots " Center'' and " Edge''. Do you see any difference in the trajectories in the two different cases of initial position. Explain.

END ACTIVITY

1.2 Temperature

What is temperature?

Our computer model is based on the kinetic molecular theory which predicts that temperature is related to the motion of a large number of particles that are continually bumping into one another. The temperature of an object is a measure of the energy of particle motion.

Energy is one of the most important concepts in science because it is essential to our existence and it cannot be destroyed. The Law of Energy Conservation is one of the most fundamental in nature and says that in any process, the total amount of energy is always conserved.

Energy is not at all easy to define because it exists in many forms that transform into one another in various chemical and physical processes. In fact, before the development of modern civilization, human beings knew how to utilize relatively few sources of energy.

Kinetic energy is one form of mechanical energy and is due to the motion of an object. The kinetic energy of an object depends only on the object's velocity v and mass m. In mathematical terms, kinetic energy can be defined by the equation:

E_k= mv²
2
.
(1.1)

Q1.20: Rank the following asteroids according to the amount of damage they would inflict on Earth during a head-on collision: (a) mass m, velocity v; (b) mass 2m, velocity v; (c) mass m, velocity 2v. Explain your answer.

According to the kinetic molecular theory the temperature, T, of a substance is proportional the average kinetic energy of the particles in the substance, so that:

T � (E_k)_avg= �
� mv²
2
�
� avg
.
(1.2)

The average kinetic energy of a large number of particles, (E_k)_avg is equal to the sum of the kinetic energies of all the particles divided by the total number of particles. A typical laboratory sample contains about 10²³ particles. Our computer model contains, at most, 200 particles.

Q1.21: Suppose we have a system of only 3 identical particles, each with mass m=1. The first has a velocity magnitude v₁=2, the second v₂=1, and the third v₃=4. Compute the magnitude of the average kinetic energy of this system. (Note: Our model uses " computer units'' where the particles are not identified as specific atoms. For exploration of units, see Feature Tour and HandsOn 34: Computer versus Real Units).

Q1.22: Now suppose we have a system of only 2 identical particles, each with mass m=1. The first has a velocity magnitude v₁=2 and the second has a velocity magnitude v₂=4. After a purely elastic collision, the velocity magnitude of the first particle becomes v₁=3. What is the velocity magnitude of the second particle?

Q1.23: If we increase the temperature, what happens to the average speed of particles v? What happens to the average kinetic energy? Explain your answers.

Q1.24: Assuming the temperature remains constant, will heavier particles move faster or slower than lighter particles? Explain your answer.

Q1.25: If temperature increases by a factor of 100, by what factor will the average particle velocity increase or decrease? Explain your answer.

The temperature equation is based on the average kinetic energies of all particles. What about each individual particle? Whatever the temperature of a substance, the movement of its particles will be chaotic and the range of their constantly-changing velocities can be quite large. It is important to study the range of velocity values. For example, in a chemical reaction, usually only the fastest molecules react when they collide.

BEGIN ACTIVITY

HandsOn 1: Observing Particle Motion in Hot and Cold Water

Nearly fill one beaker with cold water and another with hot water. Place a drop of food coloring into each beaker near the rim.

Q1.26: Describe, in drawings and in words, what you think may be happening at the molecular level.

END ACTIVITY

BEGIN ACTIVITY

SimuLab 2: Velocity Distribution

Your objective is to:

Investigate the distribution of particle velocities and its dependence on temperature and mass.
You will be able to:

Explain why, in a system at fixed temperature, particles have a wide range of velocities.

Contrast the velocity distribution of a gas at low temperature with a velocity distribution of a gas at high temperature.

Contrast the velocity distribution of heavy particles with the velocity distribution of light particles.

1. Open SMDPlayer, select Temperature from the StatesofMatter folder. Press Play. Read the captions and follow the instructions. Select File - Quit

In the introductory movie we see that the average kinetic energy of particles increases with temperature. We also see that velocities of the majority of particles increases with temperature.

2. Open SMD, select the file Temperature1 in the States of Matter folder. Press Start

Your system represents a high density gas of 200 green particles at high temperature.

Q1.27: What is the temperature of your system?

Observe the temperature graph. Go to graph panel and switch the graph to Kinetic Energies.

The green line represents the average kinetic energy of the green particles.

Q1.28: What is the average kinetic energy of the green particles?

Q1.29: Does the kinetic energy graph coincide with temperature graph? Explain.

3. Switch Display Particles by: to Absolute Kinetic Energies.

The colors of the particles indicate their kinetic energies in the rainbow order: red particles have small kinetic energies, violet particles have large kinetic energies. Observe how the velocities of the particles (and their color) change as they collide.

4. Press Pause. Set Iterations Between Displays to 50. Select Edit - Select Particles. Choose Select Particle(s) and click on any particle in the display window. Press Start.

A white rim will appear around the selected particle. You will observe changes in the kinetic energy of this particle over time.

Q1.30: Does the kinetic energy and the velocity of the selected particle remain constant? Explain.

Q1.31: Why are the velocities of the particles not equal? Why do the colors of the particles change? Explain.

5. Set Iterations between Displays to 100. Switch the graph to Velocity Distribution.

The x-axis of the graph represents the velocity and the y-axis represents the percentage of particles with that velocity. At each update of the screen, the computer program measures the velocities of all 200 particles and adds these values to the histogram.

Q1.32: Describe what happens to the histrogram of velocities as more and more velocity updates are taken into account.

6. Wait until the velocity distribution becomes a smooth curve with a well-defined maximum which usually happens when the number of velocity updates (# of obs) reaches approximately 10000. Press Pause and select Take a Snapshot - Graph and Take a Snapshot - Screen. Type the name of the picture " T=4,m=1''.

You will need these snapshots to compare the velocity distributions at different temperatures. This snapshot represents the particles of mass m=1 and temperature T=4.

Q1.33: Which velocity value corresponds to the maximum of the histogram? Predict what will happen to the velocity value for the maximum of the histogram as the temperature is lowered to T = 0.25 and T = 1

7. Hit Pause. Using the temperature scroll change the Temperature to T=0.25, and repeat Step 6, naming the snapshots " T=.25,m=1''.

8. Change the Temperature to T=1, and repeat Step 6, naming the snapshot " T=1,m=1''.

Q1.34: Do the actual positions of the maxima of the velocity distributions coincide with your predictions in Q.1.33?

9. Enlarge snapshot gallery window (by dragging bottom right hand corner). Arrange screen shots on top, velocity distributions below screen shot.

Q1.35: Compare the velocity distributions at different temperatures from the Snapshot Gallery. Explain how they are similar how they are different.

Q1.36: Compare the snapshots of the screen at different temperatures. Relate the range of colors of the particles in the screen snapshots and the width of the velocity distributions.

10. Select menu item Edit - Particles. Choose Change all particle(s) to B and click on the particle screen. You will not see a change in the particles because they are displayed in Absolute Kinetic energy mode but now you can vary the particle's mass. Using scroll bar for mass change B particle mass to 4. Set Temperature T=1. Press Start.

We will investigate how the velocity distribution depends on the mass of the particle. In our program, only the blue particles have variable mass. Green particles always have mass m=1. So in order to change a particle's mass, we have to change the particle type to B.

Q1.37: Predict what will happen to the histogram of particle velocities when the particles have mass: (a) m=4 and (b) m=0.1. Predict the positions of the maxima of the velocity distributions for each case.

11. Repeat Step 6, naming the snapshot " T=1,m=4''

12. Change B particle mass to 0.1. Repeat Step 6, naming the snapshot " T=1,m=0.1''

Q1.38: Compare the velocity distributions for different particle masses: m=1, m=4, and m=0.1. Explain how they are similar and how they differ.

Q1.39: Does the actual position of the maximum of the distribution coincide with your predictions in Q.1.37? Explain any difference.

Q1.40: Compare the snapshots of the screen (colors representing kinetic energies) with the corresponding snapshots of the velocity distributions. Explain why the colors are the same while the velocity distributions are different.

END ACTIVITY

1.3 Research Projects

We encourage you to pursue independent research projects. Science moves forward through research! Try the suggestion below or design your own. Or, feel free to write an essay using any of the questions throughout this chapter as inspiration.

BEGIN ACTIVITY

Research Project 1: States of Matter

See SimuLab 1

Explore how the decreasing of temperature affects the state of matter. In SimuLab 1, we explored how the increase of temperature lead to melting and evaporation of a substance. Is this process reversible? Will the cooling of gas leads to condensation and then to freezing? Will the process be as fast as melting and evaporation is if you just watch the movie StatesOfMatter in the opposite direction, or it will happen in a different way?

1. Open SMD and select Gas in the StateOfMatter folder. Decrease the Temperature to T=0.4. and observe what happens. You have to wait for about 2000 computer time units. To speed up the process, set Iterations Between Displays to 1000.

2. Decrease the Temperature to T=0.25 and observe the process for another 2000 time units.

3. Determine the condensation point temperature (the point at which the gas becomes a liquid) and the freezing point temperature (the temperature at which the liquid becomes a solid) by varying the temperature in the appropriate range and watching the changes in the order and in the motion of the particles.

END ACTIVITY BEGIN ACTIVITY

Research Project 2: Velocity Distribution

See SimuLab 3

Test if the velocity distribution depends on the state of matter or the density of the substance.

1. Open SMD and select Temperature2 in the StateOfMatter folder.

You are visualizing a crystal of blue particles surrounded by a gas of green particles. The crystal does not melt because in this simulation the blue particles interact much stronger than the green particles. (See Show Additional Parameters - BB interaction parameter.

Q1.41: Read the values of the Temperature and B particle mass and predict if the velocity distributions of B and G particles will coincide or differ.

2. Change Display particles by to Absolute Kinetic Energy.

Observe that the colors of particles in the gas and in the crystal are similar. This means that particles in the crystal and in the gas has the same average value, hence they have same temperatures. In other words they are at thermal equilibrium with each other.

3. To save computer time, we recommend setting Iterations Between Displays to 100 or more. Make screen and graph snapshots.

Compare velocity distributions for particles in the gas and in the crystal using Velocity Distribution for G and Velocity Distribution for B graphs and waiting until the velocity distribution for B and G particles become smooth curves with well-defined maxima.

4. Change particle mass to 0.1 and then 10. Repeat Step 3.

Predict the change in the velocity distributions.

5. Restore B particle mass =1. In the Additional Parameters window, Change Density to 0.8. Repeat Step 3.

Predict the changes in the velocity distributions.

6. Increase the Temperature to T=4. Predict the changes in the velocity distributions. Repeat Step 3.

Q1.42: Compare the snapshots of velocity distributions of B and G particles with the initial set and explain their differences and similarities. Do the velocity distributions depend on the density or state of matter? Explain your answer.

Q1.43: Compare the snapshots of the screen at different conditions.

END ACTIVITY BEGIN ACTIVITY

Research Project 3: Velocity Distribution II

See SimuLab 3

Investigate whether velocity the distribution depends on parameters other than temperature and mass of particles.

1. Open SMD, select the file Temperature2 from the States of Matter folder.

2. Keep mass of particle B and temperature constant (Heat bath on). Set Iterations Between Displays to 100 or more. Vary any other parameter in the Additional Parameters window. For example, change density, interaction parameters, boundaries, insert piston, introduce gravity. For each set of parameters obtain smooth velocity distributions for B and G particles. Make a snapshot of screens and velocity distribution graphs for different conditions. Be sure to run the program for each parameter setting long enough so that the velocity distributions are smooth.

Q1.44: Compare the snapshots of velocity distributions of B and G particles and explain their differences and similarities. Can you conclude whether the velocity distributions depend on any parameter except temperature and mass? Explain.

Q1.45: Compare the snapshots of the particle screen at different conditions and try to relate the parameter changes to what you see.

END ACTIVITY

BEGIN ACTIVITY

Research Project 4: Velocity Distribution III

See SimuLab 3

Explore how the velocity distribution aquires its shape due to particles collisions.

1. Open SMD using the default configuration. Change Display particles by to Absolute kinetic energy. Set Iterations between Displays to 100. Switch graph to Velocity Distribution. Press Start.

At the beginning all the particles are assigned the same velocity magnitude.

Q1.46: As the simulation proceeds, why does the distribution of velocities differ from the initial distribution?

END ACTIVITY

BEGIN ACTIVITY

Research Project 5: Velocity Distribution IV

See SimuLab 3

Explore how two substances in contact reach thermal equilibrium.

1. Open SMD, select the file Temperature3 from the States of Matter folder. Switch the Display Particles by to Absolute Kinetic Energies. Make a snapshot of the screen. Switch Iterations Between Displays to 100 and Press Start.

The temperature of the crystal is much smaller than that of surrounding gas.

Q1.47: Watch the graphs of the average kinetic energies of the blue and the green particles. Explain what you see on the graph and on the screen from the point of view of molecular kinetic theory.

2. Reset the experiment. Switch the graph to Velocity distribution. Collect the velocity distributions for B and G particles for 10000 observations. Make snapshots of the velocity distributions.

3. Switch the graph back to Kinetic Energies.

Wait until the average kinetic energies of green and blue particles become equal.

4. When the system reaches equilibrium, reset the velocity distribution by switching to No graph and then to velocity distribution

Collect 10000 observations. Make snapshots of the velocity distributions.

Q1.48: Collect the new set of velocity distributions. Compare them to the previous distributions from Step 2. Explain what you see from the point of view of molecular kinetic theory.

Chapter 2
Ideal Gases

Many chemical reactions are accompanied by the formation of a gas or occur entirely in the gaseous state. Measuring gas parameters, such as volume and temperature, gives information about the stoichiometry of the reaction and the energy transformation that accompany the reaction. The gas parameters are: pressure, volume, temperature and density. These parameters do not change independently, but are linked together and described quantitatively by the gas laws. The idea that gases consist of a large number of tiny particles moving randomly in all possible directions provides the modern explanation for the gas laws and is the foundation of the Kinetic Molecular Theory.

2.1 The Concept of Pressure

It is interesting to note that at times gas sample can behave like a solid!. For example think of an inflatable mattress and a second mattress with coil spring. The air in the inflatable mattress serves the same function as the coils in the second mattress. In both cases when pressure is applied the mattresses deform (are compressed). When pressure is removed the mattress returns to their original shape (volume).

In the following demonstration you will see how air behaves like an elastic coil spring.

BEGIN ACTIVITY

HandsOn 2: Tire Pump and Coil Spring

You will need:

a spring.

Q2.1: Do you feel any resistance as you push the piston? Try to explain your observation.

Q2.2: What happens and how do you explain it?

Q2.3: Do you feel any resistance? Propose an explanation.

Q2.4: Do you feel any resistance as you pull the piston? Try to explain your observation. Clue: repeat the experiment without dosing the nozzle.

Q2.5: What do you feel? Propose an explanation.

END ACTIVITY

We observed in the preceding HandsOn activity that a gas behaves much like a coiled spring. If a certain force is applied to the piston, the volume of a gas under the piston is reduced. If this force is removed, the gas expands.

In the quantitative study of such elastic properties of the air, one of the greatest contributions was made in the second half of 17th century by the Irish chemist Robert Boyle (1627 - 1691). He discovered that although a force is what is acting on the piston, the amount of force applied per unit of area is the essential parameter. Boyle was talking about the concept of pressure. Boyle performed quantitative experiments to measure the relationship between the pressure and volume of air.

Pressure is the ratio of the force to area over which it is applied.

Pressure= Force
Area

Pressure is measured in Pascals. One Pascal equals the pressure created by a force of one Newton distributed over the area of one square meter. If you are wondering how much one Pascal is, it is roughly equivalent to the pressure created by a piece of paper lying on your kitchen table.

When we applied force to solid objects, they deform. However the magnitude of the deformation depends not on the force, but rather on the pressure. To reduce the pressure on your shoulders, the straps of your backpack are made wide. Imagine how uncomfortable it would be if the straps were made of thin ropes. If the deformation is not too high, if the force is taken away, the solid returns to his original shape. The most common example of an elastic object is a coil spring. Coils springs are used in mattresses. When you sit down the coil spring shrink, when you stand up the mattress returns to its original shape.

Q2.6: Assume the pressure caused by a book balanced on your finger is P. If you were to balance the same book on your hand (with an area 50 times that of your finger), what would this new pressure be?

Q2.7: Calculate the pressure caused by a 1 Kg book if balanced on your palm (area approximately 1.5 ×10^-2 m²) vs. the pressure created by this same book balanced on your index finger (area approximately 3 ×10^-4 m²).

We can conclude from this example that the pressure of a given force distributed over a small surface is much greater the pressure distributed over a large surface.

One of the most commonly encountered examples of pressure is that of the atmosphere. The atmosphere exerts pressure on any object on the surface of the Earth. Atmospheric pressure at sea level is 101,000 Pascals. This means that the air presses down on 1 square meter surface with the magnitude of 101,000 Newtons, which is approximately equivalent to the weight of 10,000 kilograms. The following experiment will allow you to understand the relative magnitude of atmospheric pressure.

BEGIN ACTIVITY

HandsOn 3: Atmospheric Pressure

CAUTION: Do not do this without teacher supervision. Goggles and gloves are highly recommended.

You will need:

a microwave oven

oven mitts or winter gloves.

off

Q2.8: What do you see and how do you explain it? Clue: In this experiment the atmospheric pressure remains the same but the pressure inside the bottle drops when we cool it down.

END ACTIVITY

2.2 Boyle's Law

While performing several experiments, Robert Boyle determined that at constant temperature the volume of a gas is inversely proportional to the pressure: V 1/P, or in other words, product of P times V remains constant when both of these variables change

PV=const.

In this equation, the constant depends on the temperature of the gas sample and the number of gas particles. The higher the pressure, the smaller the volume occupied by the gas.

BEGIN ACTIVITY

SimuLab 3: Qualitative Investigation of Boyle's Law

Gas creates pressure because its particles collide with the walls of their container. The concept of moving gas molecules is the foundation of the kinetic molecular theory.

Your objective is to:

Recognize the effect of molecular collisions with the piston on the piston's position.
You will be able to:

Predict what happens to the position of the piston when the external pressure is greater than the internal pressure of the gas.

Explain why the position of the piston fluctuates when the external and internal pressures are approximately equal.

Describe gas pressure in terms of molecular collisions.

State the relationship between frequency of collision and the volume of a given gas sample.

1. Open SMDPlayer, select IntroBoyle'sLaw in the IdealGas folder. PRESS Play. Read all the captions, and follow the instructions. Go to File - Quit

Movie gives a preliminary understanding of Boyle's law from a microscopic point of view.

2. Open SMD, select Boyle-Preliminary in the IdealGas folder.

You see 200 green gas molecules under a piston represented by a red bar, as shown in Figure 2.1. Note that the Heat Bath is on, which means that the temperature of the system is kept relatively constant throughout the experiment. The system is NOT thermally isolated.

3. Set Iterations Between Displays to 10. Select Display Particles by Trajectories and press Start.

The particles start to move along straight lines with various velocities. They change their trajectories when they collide with the piston or each other.

4. Click back to Display Particles by Particle Type and observe the Volume versus Time graph.

The external pressure acting on the piston accelerates it downward, reducing the volume of the gas. In the absence of collisions with the piston, a graph of volume versus time is a smooth parabola because the piston falls freely. However, when a molecule collides with the piston, the piston's velocity instantly changes and the graph as a whole changes into a set of parabolic segments. The connections of parabolic segments illustrate numerous collisions that create internal pressure which pushes the piston upward.

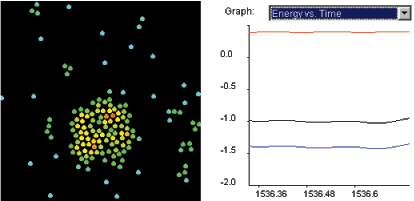
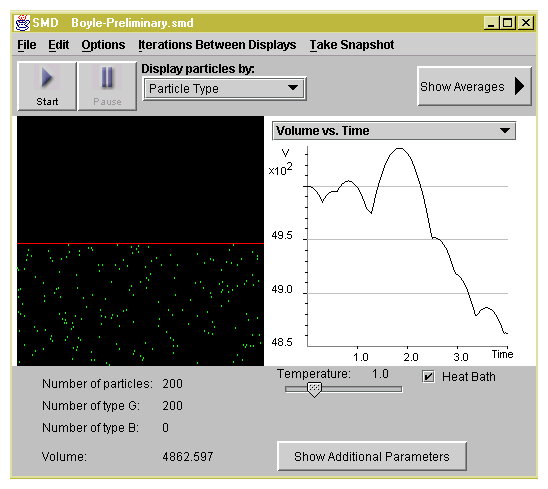Figure 2.1: Screenshot of Boyle's Law SimuLab.

5. Watch the graph for approximately 4 time units (until the graph fills the screen) and then press Pause. To copy the graph to the " Snapshot Gallery'' select Take Snapshot :Graph.

Determine the number of particle collisions with the piston by counting the number of parabolic segments as shown in Figure 2.2.

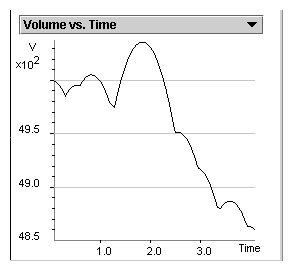Figure 2.2: Determining the number of molecules collisions with the piston by counting the parabolic segments. The end of a parabolic segment is indicated by a jaggedness in the curve. When the number of parabolic segments is unclear-estimate. In this graph, there are 7 or 8 collisions (parabolic segments).

Q2.9: How many collisions with the piston (i.e., parabolic segments) did you count?

6. To speed up the program, set Iterations Between Displays to 1000 and press Start. Run the program for 200 time units (read Time from Averaging Window).

At equilibrium, the internal pressure created by the gas molecules colliding with the piston, should be equal to the external pressure, which is set at 0.04. The internal pressure value can be found in the Average Values panel. The external pressure value can be found in the Additional Parameters window by selecting Show Additional Parameters. Read the volume of the gas from the Average Values panel and record it. While running this simulation answer the following questions:

Q2.10: Notice that relatively few particles collide with the piston at any particular moment. Will this cause the internal pressure to (a) stay the same, (b) fluctuate a little, or (c) fluctuate greatly? Explain your reasoning.

Q2.11: If the external pressure is greater than the internal pressure, what will happen to the piston?
If the external pressure is less than the internal pressure, what will happen to the piston?

Q2.12: If the internal pressure is averaged over an extended period of time and we wait until the system comes to equilibrium, will the average internal pressure be (a) higher, (b) lower, or (c) equal to the external pressure? Explain your reasoning.

Q2.13: At equilibrium, what happens to the piston?

Q2.14: What happens to the volume of a gas at equilibrium? Does this happen in our simulation?

Q2.15: What role, if any, does the number of particles in our simulation have on the fluctuations in volume at equilibrium?

Q2.16: Describe the equilibrium state for a gas contained in a container with a piston.

7. Press Pause. Double the External Pressure to 0.08.

Q2.17: According to Boyle's Law, predict what should happen to the average volume when we double the external pressure.

8. Select Reset Averages on the Average Values panel. Press Start.

By resetting averages you eliminate the data from the previous stage of the experiment when the pressure was 0.04.

Q2.18: Describe what happens to the piston position and explain why. What happens to the volume of gas?

9. Select the Pressure versus Time graph on the Graph panel. When the internal pressure value displayed on the graph is approximately equal to the external pressure, press Pause. Record the volume of the gas from the main window.

You are observing the gas system approaching equilibrium where the internal and external pressure are approximately equal.

Q2.19: How does the volume you recorded compare to your prediction? To what extent are the simulation results consistent with Boyle's Law?

10. Set Iterations Between Displays back to 10. Select the Volume versus Time graph on the Graph panel. Press Start. Watch the graph for approximately 5 time units (until graph fills the screen). Press Pause. Copy the graph to the " Snapshot Gallery'' by selecting Take Snapshot : Graph.

Determine the number of particle collisions with the piston by counting the number of of parabolic segments, which represent the number of particle collisions with the piston.

Q2.20: How do the two graphs compare in terms of the number of parabolic segments? Propose an explanation for the observed 1 to 2 ratio.

Q2.21: How does the change in volume relate to the frequency of collisions with piston?

Q2.22: How does the change in frequency of collisions relate to the change in internal pressure?

END ACTIVITY

BEGIN ACTIVITY

SimuLab 4: Quantitative Investigation of Boyle's Law

Your objective is to:

Test that the product PV remains constant for several positions of the piston at constant temperature.

You will be able to:
State Boyle's Law.

Construct a P versus V graph from collected data.

Construct a P versus 1/V graph.

Contrast the two curves.

Explain the significance of the slope on the P versus 1/V graph.

Predict what will happen to the PV product if the temperature is changed.

Construct a P versus number density graph.

Reformulate Boyle's Law in terms of gas density.

1. Open SMD, select Boyle1000 in the IdealGas folder.

You will see 200 particles compressed in a container whose volume is fixed at 1000. The Temperature is set at 1.25 and the Heat Bath is on (i. e. the temperature is maintained at a relatively constant value).

2. Press Start.

The molecules start to move and bump into the walls of the container. The graph panel represents the internal pressure created by 200 gas particles at a given moment.

Q2.23: How do you explain the relatively large fluctuations in the pressure of the system?

3. Select Show Averages.

Observe the time and the other values carefully.

Q2.24: Wait for about five time units. Do you notice any change in the fluctuations of the pressure values in the Average Values panel?

4. Change Iterations Between Displays to 500. Let the program run for approximately 20 time units. Press Pause.

In order to obtain accurate value for pressure we need to average data over a longer period of time. Iteration setting of 500 speeds up the simulation.

5. Record temperature, number density, volume, and pressure data from the Average Values panel into the table. Calculate the PV value.

You will need these data for further analysis.

Table I

Volume 1000        2000        4000       8000       10,000

Temperature

Number Density

Pressure

PV

Deviation from average

% deviation

Calculate (PV)_ave value = �_i=1⁵ P_i V_i :________

Deviation from average = | (P V)_i - (P V) _avg|

% deviation = (|(PV)_ave-P_iV_i|)/((PV)_ave) x 100

Calculate average % deviation = �_i=1⁵(|(PV)_ave-P_iV_i|)/((PV)_ave) x 100 value:________

6. Select File : Open Preset Experiment and open Boyle2000. Press Start. After approximately 20 time units press Pause. Record the values and calculate the PV value as described in Step 5.

In order to test Boyle's law, we will measure the pressure of the same amount of gas at the same temperature and different volumes.

7. Repeat Steps 6 for Boyle4000, Boyle8000, and Boyle10000.

Q2.25: Compare the values of PV for various volumes. Find the average value of these products and calculate the deviation of each PV value from the average. Calculate the percent deviation of each ( PV) _i value from the average (PV) _ave by using this formula:

%_deviation = �
� | (PV)_i-(PV)_ave|
(PV)_ave
×100 �
�

Find the largest percent deviation.

To what extent are your results consistent with Boyle's Law? Hint: Refer to your percent deviation and range of values of pressure.

Q2.26: Construct a Pressure vs. Volume graph. This plot represents the dependence of pressure on volume at constant temperature. According to Boyle's law, when the temperature is constant, the graph should be a hyperbola.

If your graph varies significantly from a hyperbola, do you have any idea why this may have been so?

Q2.27: Construct a Pressure vs. 1/Volume graph. Draw the line of best fit through the data points. Determine the slope of this line and compare it to the average PV product in the above chart.

What is the relationship between the slope and the average PV product?

What is the difference between the graph of P vs. 1/V and the graphs of P vs. V graph?

Q2.28: Construct a Pressure vs. Number Density graph. Number Density is defined as Number of particles over volume: n = N/V. The distribution of data points should fall as a straight line.

What is the relationship between pressure and number density?

Compare this graph to the Pressure vs. 1/Volume graph. We should now be able to state an alternative form of Boyle's law: at constant temperature, the gas pressure is directly proportional to the gas number density.

Q2.29: Find the slope of the Pressure vs. Number Density graph and comment on the relationship between the slope and temperature of the system.

Q2.30: Graph the PV product vs. Pressure.

What slope do you expect? What do you find? Explain the deviation from your prediction (Hint: consider that ideal gas behavior is followed at low pressures and high temperatures).

END ACTIVITY

2.3 Temperature

BEGIN ACTIVITY

HandsOn 4: The Subjective Sensation of Temperature

⁰

Q2.31: Is water in the middle bowl hot or cold? Explain.

From this simple experiment, you have hopefully discovered that the hand is not an accurate thermometer. Galileo observed that almost all substances expand when they are heated. This insight led to the construction of the first thermometer.

END ACTIVITY

BEGIN ACTIVITY

HandsOn 5: HandsOn: Galileo's Thermometer

We can try to duplicate Galileo's thermometer with the aid of everyday household items.

You will need (as shown in Figure 2.3):

a cork that fits the bottle

a thin glass tube about 10 inches long (you can use a transparent plastic straw if you do not have a glass tube)

a drill with drill bit slightly smaller than the diameter of the tube

Figure

Figure 2.3: Schematic of Galileo's Thermometer experiment.

Q2.32: What happened to the plug of liquid?

Q2.33: How would you increase the temperature range of your thermometer?

END ACTIVITY

BEGIN ACTIVITY

SimuLab 5: Galileo's Thermometer - Movie

Due to the small number of particles in our system it would take a very long time for a liquid droplet in a tube to reach thermal equilibrium. To reduce the time of this activity, we will explore a movie of the simulation.

Your objective is to:

Understand the principle of how a thermometer works in terms of molecular motion.

You will be able to:
Explain how a thermometer works in terms of molecular motion.

Explain why the column of liquid goes down as temperature is decreased.

1. Open SMDPlayer, select Galileo-Thermometer in the IdealGas folder. Press Play.

The movie pauses at the opening frame and displays the first explanatory caption. In order to better visualize the particles, you can select Edit : Background White. The narrow column on the screen represents our thermometer tube, blue particles represent air molecules, and the green layer represents a liquid droplet.

2. Press Play to resume the movie. The movie pauses at each explanatory caption. Repeat this step until the end of the movie is reached.

At a given temperature, the droplet fluctuates around a certain equilibrium position. Each time the temperature drops in our simulation, the equilibrium position of the green layer also drops. Near the end of the movie, we simulate the effect of the thermometer inserted into an extremely hot environment: everything is thrown out of the tube and your thermometer breaks!

Q2.34: Describe the relationship between the height of the gas sample and the temperature. Explain how the thermometer works in terms of molecular motion.

END ACTIVITY

2.4 Charles Law

A century after Boyle derived his law, the French scientist Jacques Charles (1746 - 1823) discovered a linear relationship between gas temperature and gas volume when pressure is kept constant. Using a temperature versus volume graph, he discovered that the volume of any gas at constant pressure would approach zero at -273⁰C. He did not publish these results. Twenty years later, another French chemist, Joseph Gay-Lussac, repeated Charles' experiments, got the same results, and published them. At that time, however, no one could even get close to -273⁰C in a laboratory, so Gay-Lussac could only determine his law by extrapolating the volume line on his graph until it crossed the temperature-axis. Later, this temperature was called absolute zero. The name for the new temperature scale, which has the origin at absolute zero, is the Kelvin scale. Zero degrees in Kelvin corresponds to -273⁰C and is the temperature at which all molecular motion ceases.

In the next simulation we will demonstrate Charles' Law from a microscopic point of view. We will put a gas in a cylinder under a piston and keep the external pressure constant. Imagine that this pressure is created by a constant weight resting on top of the piston. At any given temperature, the particles have a certain average velocity. They collide with the piston and the walls of the cylinder, thus, causing pressure. If the temperature is lowered, the average velocity of the particles decreases, and the particles collide with the piston and cylinder walls less frequently and with less force and thus the internal pressure drops. Since the weight resting on top of the piston remains constant, the piston descends until the pressure inside the cylinder becomes equal to the external pressure, therefore reaching equilibrium again. As the volume of the gas decreases the number of collisions with the walls increase and thus the internal pressure increases. Since we only have 200 particles in this simulation, there are relatively few collisions with the piston, and the piston constantly moves up and down. In a real experiment, with 10²³ or more molecules in a sample, the drumming on the piston produced by such a great number of molecules is constant and would not lead to macroscopic oscillations, and the piston, after a few initial initial oscilations stays almost constant.

BEGIN ACTIVITY

SimuLab 6: Charles' Law - Movie

Your objective is to:

Recognize the microscopic origin of the volume variations with temperature at constant external pressure.

You will be able to:
State Charles' Law.

Construct a volume versus temperature graph from collected data.

State the relationship between volume and temperature.

Determine the temperature at which the volume would be zero and explain the significance of this point.

Propose reasons as to why the V/T value deviates from predictions of Charles' Law.

State the relationship between number density and temperature.

1. Open SMDPlayer, select Charles in the IdealGas folder. Select Show Averages. Press Play to resume the movie. The movie pauses at each explanatory caption. Follow the instructions in each caption, making sure to Reset Averages in the Average Values panel. Repeat this step until the end of the movie is reached. If you wish to see the temperature in Kelvin scale press Real Units button.

Notice that the average pressure stays approximately the same throughout the entire movie. Note that the temperature throughout the movie decreased by a factor of 2.5. In our simulation, the temperature of the gas sample is equal to the average kinetic energy of the molecules. The average kinetic energy is proportional to the average velocity squared (E_k=( (mv²)/2) _avg). Therefore, the average velocity is decreased by �{2.5} � 1.6. Did you notice that the particles move slower at the end of the movie than at the beginning? To compare, you can watch the movie again.

	T₁	T₂	T₃	T₄	T₅
Temperature
Pressure
NumberDensity (N/V)
Volume
V/T
Deviation from average
% Deviation

Calculate average ( V/T) _avg value = �_i⁵ (V_i)/(T_i) : ______________

Deviation from average = |( V/T)_i -( V/T)_ave|

% Deviation = (|( V/T)_i -( V/T)_ave|)/(( V/T)_avg) ×100

Q2.35: Plot Volume vs. Temperature on a graph. Draw a line of best fit through the points.

Q2.36: What is the relationship between volume and temperature?

Q2.37: On a Volume vs. Temperature graph, for an ideal gas the line intersects the temperature axis at the origin. Comment on the extent to which your graph is consistent with Charles' Law.

Q2.38: Compare the values of V/T for various temperatures. Find the average value of these ratios and calculate the deviation of each V/T value from the average. Calculate the percent deviation of each ( V/T) _i value: and calculate the average percent deviation.

Q2.39: Plot the Number density vs. Temperature graph.

Q2.40: How does number density vary with temperature?

END ACTIVITY

2.5 Gay-Lussac Law

Joseph Gay-Lussac (1778-1850) continued investigating gases and performed an experiment in which he changed the temperature and kept the volume constant. He found that at constant volume the pressure increases linearly with temperature. The graph of pressure vs. temperature is a straight line. The slope of this line depends on the volume of the gas sample and on the number of gas particles. For various volumes the lines, when extrapolated, cross approximately at the point P = 0, T = -273⁰C on the graph. This point corresponds to the same temperature as in the Charles' Law graphs where pressure was held constant. At this temperature the gas exerts no pressure at all. Later this temperature was called absolute zero, and a new temperature scale called Kelvin was established. Zero degrees Kelvin, corresponds to -273⁰C. Gas pressure is created by collisions of particles with the walls, therefore at absolute zero the particles of gas should completely stop moving. In terms of the Kelvin temperature scale, the Gay-Lussac law can be written as

P
T
=const,

where the constant depends on the volume and the number of gas particles.

BEGIN ACTIVITY

SimuLab 7: Gay-Lussac Law

Your objective is to:

Recognize the microscopic origin of the internal pressure variations with temperature at constant volume.

You will be able to:
State Gay-Lussac's Law.

Construct a Pressure vs Temperature graph.

Extrapolate the slope on the graph to P=0 and explain the significance of this point.

Determine the temperature range at which data is consistent with Gay-Lussac Law.

Suggest reasons why deviations from Gay-Lussac Law occur.

  T=4     T=3     T=2     T=1.25     T=1

Pressure

P/T

Deviation from ave.

% deviation

Average P/T value: _____________

1. Open SMD, select Gay-Lussac in the IdealGas folder.

You see 200 gas molecules in a fixed volume, the temperature is T = 4.0 and the Number Density ( N/V) = 0.02 (number of particles divided by volume).

2. Select Show Averages. Press Start. Watch the Pressure vs. Time graph for approximately 5.0 time units.

You can see that the fluctuations of pressure are rather significant and the values on the Average Values panel are constantly changing. In order to obtain accurate measurements, you need to average data for significantly longer times, such as 20 time units.

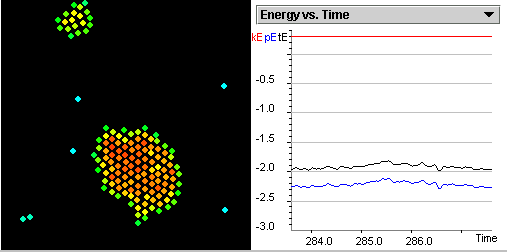
3. Change Iterations Between Displays to 500. Let the program run for approximately 20 computer time units as shown in figure 2.4. Press Pause.

Setting Iterations Between Displays at 500 speeds up the simulation.

figures2/pic4c.png

Figure 2.4: Screenshot of Gay-Lussac's Law SimuLab.

4. Record the pressure from the Average Values panel for this trial in your Table for T=4. Calculate the P/T value. Press Reset Averages on the Average Values panel.

You are preparing data for the future analysis.

5. Set the Temperature to T=3. Press Start. Let the program run for 20 time units. Press Pause. Record Pressure and calculate P/T ratio. Select Reset Averages on the Average Values panel.

Ressetting Averages allows you to delete the data values from the previous experiment.

6. Repeat Step 5 for Temperatures T=2, T=1.25,and T=1.

Q2.41: Compare the values of P/T obtained for various temperatures with the average value of P/T from the table. | ( P/T)_i - ( P/T )_avg |. Express the differences in percents

�
� �
� P
T
�
� i
- �
� P
T
�
� avg
�
�

�
� P
T
�
� avg
×100

and record them into the table.

Q2.42: What conclusions can you draw about the consistency of the P/T constant in relation to temperature?

Q2.43: Plot a Pressure vs. Temperature graph. Approximate it by a straight line. Determine the slope of the graph. Extrapolate the line to P=0.

Q2.44: What is the temperature when P=0? Explain your result.

END ACTIVITY

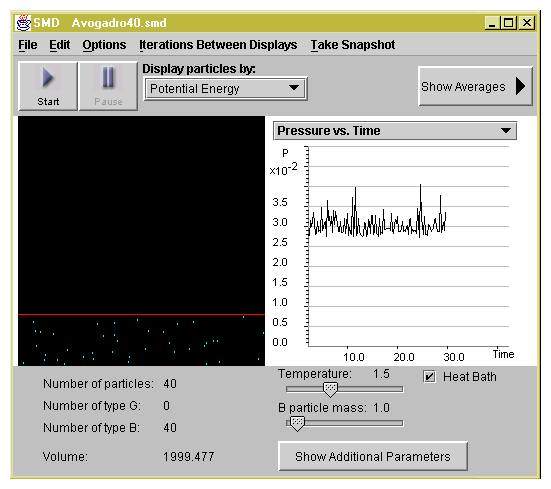
2.6 Avogadro's Law

In 1809, Gay-Lussac performed several experiments with reacting gases showing that under constant conditions of pressure and temperature, volume was not necessarily a conserved quantity. In other words, if you start out with three volumes of gas, you won't necessarily end up with three volumes at the end of a chemical reaction; mass is conserved in a chemical reaction, volume is not. For example, if two volume units of hydrogen gas are mixed with one volume unit of oxygen gas at constant pressure, the water vapor produced by the reaction occupies two volume units

2H_{2( gas)}+O_{2( gas)}� 2H₂O_(gas).

In this example, the number of atoms (i.e., mass) is conserved on each side of the equation but the volume of gas is not conserved.

Two years later Italian scientist Amadeo Avogadro (1776-1856) explained these results by stating that in equal volumes of any gas at the same temperature and pressure there are equal numbers of particles. The name of the unit that represents a certain fixed number of particles is a mole. One mole contains the Avogadro number N_A of molecules, N_A=6.02·10²³. Then we can reformulate the Avogadro law: at constant temperature and pressure the volume of gas is proportional to the number of moles of gas particles:

V
n
=const

Remembering that molecular collisions with the sides of a container cause pressure, then for a chemical reaction performed in a container of constant volume the Avogadro law gives: at constant temperature and volume the pressure is proportional to the number of moles of gas.

P
n
=const

BEGIN ACTIVITY

SimuLab 8: Avogadro's Principle

Your objective is to:

Recognize the role of the number of moles (here the number of particles) in the determination of the internal pressure of a gas.

You will be able to:
State the relationship between the number of particles and the volume they occupy if pressure and temperature remain constant.

Calculate the volume when temperature and pressure remain constant.

State Avogadro's hypothesis.

Contrast number density to mass density.

Predict what happens to each parameter if the number of particles is doubled.

      T             P             V             N       (# of particles)    mass

Avogadro40

Avogadro200

Avogadro100

Avogadro100

1. Open SMDPlayer, select IntroAvogadro'sLaw from the Ideal Gas folder. PRESS Play. Read all the captions and follow the instructions. Go to File - Quit

Movie gives a preliminary understanding of Avogadro's Principle from a microscopic point of view.

2. Open SMD, select Avogadro40 in the IdealGas folder. In order to better visualize the particles, you can select Edit : Background White. To speed up the simulation, change the Iterations Between Displays to 1000. Select Show Averages.

In this experiment you are visualizing 40 particles (displayed as a B particle type), each of which has a mass of 1.0 unit.

3. Press Start. Observe the Pressure versus Time graph for approximately 40 time units as shown in figure 2.5. Press Pause.

The gas is approaching equilibrium. The pressure fluctuates around an average value.

figures2/pic5c.png

Figure 2.5: Screenshot of Avogadro's SimuLab.

4. Record the temperature T, pressure P, volume V, number of type B particles N, and the B particle mass m.

You are collecting data for future analysis and recording it in the first row of the data table.

5. Open Avogadro200 by selecting File - Open Preset Experiment.

In this experiment you are visualizing 200 particles of mass 1.0. Note that the piston is now above the screen and you can not see it.

6. Repeat Steps 3 and 4.

You are collecting data for future analysis and recording it in the second row of the data table.

Q2.45: Are there any changes in parameters other than the number of particles? If so, what are they?

Q2.46: What is the relationship between the number of particles and the volume they occupy if pressure and temperature remain the same?

Q2.47: What do you predict the volume to be if you have 100 particles, each with a mass of 1.0?

7. Open Avogadro100 by selecting File - Open Preset Experiment.

This simulation contains 100 particles of mass 1.0.

8. Repeat Steps 3 and 4.

You are collecting data for future analysis and recording it in the third row of the data table.

Q2.48: Speculate: What do you think will happen if we increase the mass of the particles? Why? To test your speculation, move onto the next steps.

9. Select File - Reset Experiment. Set B particle mass to m=10.

Now this simulation contains 100 particles of mass 10.0.

10. Repeat Steps 2 and 3.

You are collecting data for future analysis and recording it in the fourth row of the data table.

Q2.49: What happened to the parameters of temperature, pressure, and volume when you changed the mass of the particle?

Q2.50: In our simulations, " density'' always refers to number density N/V. The density which you are probably most familiar with is mass density M/V= mN/V; where M is mass, V is volume, m is mass of a single particle and N is the number of particles.

What happens to the number density when the B particle is set to a mass of m=10 in Step 7?

Q2.51: What happens to the mass density when the B particle is set to mass m=10? Contrast this to the Number Density above and explain.

Q2.52: What do you predict the volume would be for 175 particles of Mass=5?

Q2.53: Consider two 1-liter balloons at room temperature. One balloon is filled with one mole of He gas and the other with one mole of Ne gas. How do their pressures, mass densities, and number densities compare?

END ACTIVITY

BEGIN ACTIVITY

SimuLab 9: Avogadro's Principle Movie

Your objective is to:

Investigate the relationship between the number of gas particles and the volume they occupy if temperature and pressure are kept constant.

You will be able to:
State the relationship between the number of particles and the volume they occupy if pressure and temperature remains constant.

State Avogadro's hypothesis.

Contrast mass density with number density.

Explain the relationship between volume, number density and mass density in terms of Avogadro's Principle.

1. Open SMDPlayer, select Avogadro in the IdealGas folder.

You see a mixture of gases under a piston. Follow the instructions in the captions.

2. Press Play. The movie pauses at the opening frame and displays the first explanatory caption. Select Show Averages. The movie pauses at each explanatory caption.

The Averages panel displays average (not instantaneous) values of the parameters as the experiment proceeds.

3. Press Play to resume the movie after each caption. Be sure to reset Averages when instructed to do so thus eliminating data from previous setting.

Q2.54: What has happened to the total number of particles as the product molecules are formed?

Q2.55: If the temperature and the pressure of the system are kept constant, what will happen to the volume as the number of gas particles decreases?

Q2.56: What happened to the mass density of the gas? Explain.

Q2.57: What happened to the number density? Explain.

Q2.58: Explain the changes in volume, number density, and mass density in terms of Avogadro's Principle.

END ACTIVITY

2.7 Ideal Gas Law

We arrive at the gas state equation by combining Boyle's Law, Charles' Law, Gay-Lussac's Law, and Avogadro's Principle:

PV
NT
=k.

where k=1.38·10^-23J/K is the Boltzmann constant and N is the number of particles in the gas. Usually we use moles instead of number of particles, because the number of particles is huge in typical laboratory gas samples while the numbers of moles have reasonable values. In a mole there is the Avogadro number N_A of molecules. If the number of moles in the gas sample is n, then N=N_A n is the number of particles. If we define R=kN_A we can rewrite the gas equation as:

PV=n N_AkT

PV=nRT

where R=8.31J/(K·mole) is the so called universal gas constant and n is the number of moles of gas. The above equation is called the ideal gas law. It is valid only if the gas possess " ideal'' properties:

Gas particles do not interact with each other.

An Ideal gas is not real, but rather a hypothetical substance. Real gas molecules, however, do have a tiny volume and do interact with each other. Therefore there are always deviations from the Ideal Gas Law. When conditions are close to " ideal'' (i.e., at low pressures and high temperatures) the deviations are very small. Often, though, conditions are " less than ideal''. This occurs when any of the ideal gas properties above fails to be true. For example, at low temperatures we can not neglect the interaction between the molecules which lead to phase transitions.

Q2.59: What kind of virtual experiment would you perform to determine if you are modeling a real or ideal gas?

END ACTIVITY

BEGIN ACTIVITY

SimuLab 10: Ideal Gas Law

Your objective is to:

Test the ideal gas law by obtaining V, T and P measurements and evaluating the consistency of the PV/NT ratio at various conditions.

You will be able to:
Test the validity of the ideal gas law at low densities and high temperatures.

Define the Boltzmann constant.

Test that the ideal gas law is valid for various molecular masses.

Find the limits of the ideal gas law in terms of gas density and temperature.

1. Open SMD, select IdealGasLaw in the IdealGas folder. To better visualize the particles, select Edit: Background Gray.

You are visualizing a gas mixture that consists of 100 green and 100 blue particles as shown in figure 2.6. You will perform three experiments (set ups A, B and C).

figures2/pic7c.png

Figure 2.6: Screenshot of the Ideal Gas Law SimuLab.

2. Set Iterations Between Displays to 1000. Select Show Averages.

Higher number of Iterations Between Displays speeds up the program.

3. Press Start and wait for approximately 20 time units. Press Pause. Record temperature T, pressure P, volume V, number of particles N (set-up A in your table). Calculate number density N/V and PV/NT.

The system has reached the equilibrium and you are collecting data for further analysis.

Table I

      T        P         V       N        N/V        PV/NT

A

B

C

Set-up A: 100 green particles, 100 blue, mass = 1

Set-up B: 100 green particles, mass = 1

Set-up C: 100 blue particles, mass = 10

4. Select File - Reset Experiment. Select Edit - Particles and choose Remove all B particles (blue particles) and click on the display window to take this action. Select Reset Averages in the Average Values panel. Repeat Step 3, using set-up B in your table.

Resetting Averages eliminates the data from previous experiments. You are now collecting data for this experiment.

5. Select File - Reset experiment. Select Edit - Particles and choose Remove all G which removes all green particles. Set the B particle mass to 10. Select Reset Averages in the Averages Values panel. Repeat Step 3 using set-up C in your table.

Q2.60: Compare the values of PV/NT found in set-ups A, B, and C. Calculate the average value which represents the Boltzmann constant in computer units.

Theoretically, the Boltzman constant is 1.0 in our computer simulation. In set-up A the gas density is 0.02 and is too high to give the theoretical value. In set-up B and C, the gas density is 0.01 and approaches ideal behavior.

6. Select File - Reset experiment. Select Edit - Particles and choose Change all particles to G (making all particles green).

You are preparing experimental set-up D.

7. Select Show Additional Parameters. Using scroll bar and / or arrow key, set Number Density to 0.1. Press Start. Wait approximately 10 time units so that equilibrium is reached.
At this point, Reset Averages in the Average Values panel and wait another 20 time units. Press Pause. Record parameters in your table and compute N/V and PV/NT.

You are watching the approach to equilibrium and collecting data for set-up D when equilibrium has been reached.

Table II

    T        P        V         N        N/V          PV/NT

D

E

F

Set-up D: 200 green, N/V=0.1

Set-up E: 200 green, N/V=0.2

Set-up F: 200 green, N/V=0.5

Q2.61: How does your ratio PV/NT compare to the theoretical value of 1.0?

8. Repeat Step 7 for Number Density 0.2 and 0.5.

You are collecting data for set-ups E and F.

Q2.62: Comment on the consistency of the PV/NT ratio as number density of the gas increases.

Now we will determine the range of temperatures for which the ideal gas law equation is valid.

9. To configure setup G : set Number Density to 0.02.

You are creating a very low density gas. You can choose the option " distribute particles instantaneously'' to save time.

10. Set Temperature to 2. Press Start. Wait approximately 10 time units so that equilibrium is reached. At this point, Reset Averages in the Average Values panel and wait another 20 time units. Record parameters in your table and compute PV/NT in the data table.

You are collecting data for set-up G. Resetting Averages eliminates data from when the system was not yet at equilibrium.

Table III

    T        P        V        N        N/V        PV/NT

G

H

I

Set-up G: 200 green, T=2

Set-up H: 200 green, T=1

Set-up I: 200 green, T=0.5

11. Repeat Step 10 for temperatures 1 and 0.5.

You are collecting data for set-up H and I.

Q2.63: How consistent is the PV/NT ratio when the temperature is varied in set-ups G, H, and I? Comment on conditions necessary for ideal gas behavior.

END ACTIVITY

Consequences of the Ideal Gas Law

When we decrease temperature at constant volume, the velocity of the particles decreases. If the volume is kept constant, they collide less frequently and exert less force on the walls of the container. This is consistent with Gay-Lussac's law: P/T=const. At absolute zero the particles have a velocity of zero, they do not collide with the walls of the container, and the internal pressure is zero.

If the external pressure is kept constant and the temperature is lowered, the volume of the gas decreases. At the lowered temperature, the molecules move slower, therefore collide less frequently. As a result, the internal pressure decreases. Since the external pressure is constant, the gas volume decreases until the number of collisions results in an internal pressure which is equal to the external pressure. We are assuming that gas particles have no volume and the pressure is only generated by collisions with container walls. We also assume that the volume of a gas will reach zero at absolute zero. This is consistent with Charles' law: V/T=const.

When we increase the number of particles and keep temperature and external pressure constant, the number of collisions increases and the gas expands. This is consistent with Avogadro principle for the case when P is constant and T is constant: V/n=const. When V is constant and T is constant we obtain P/n=const.

A mole of any gas at standard temperature and pressure (STP), i.e. 0⁰C temperature and pressure of 1 atm, occupies RT/P= 8.31 ×273/101,000 = 0.0224 m³=22.4 liters. The universal gas constant is commonly measured in the units of R=0.082 liters × atm/Kelvin × mole or 8.351J/Kmol.

2.8 Dalton's Law

Until this point, the assumptions of the ideal gas model effectively provided the prediction of the gas behavior at low densities and high temperatures. We can try to extend the model in order to predict the pressure produced by a mixture of various molecules. Since we define molecules as noninteracting particles of zero volume, all of them would move in the container independently. They would collide with the walls and produce pressure. The molecules of a particular kind cause a pressure that is unaffected by the presence (or absence) of other molecules. This is called the partial pressure of that gas. The molecules of another kind would produce its own partial pressure, and so on. Then the total pressure in the container is the sum of all these partial pressures. This statement is known as Dalton's Law of Partial Pressures:

P=P₁+P₂

where P is the total pressure, and P₁ and P₂ represent the partial pressure of Gas 1 and Gas 2.

BEGIN ACTIVITY

SimuLab 11: Dalton's Law

In our simulation it is more convenient to use number of particles instead of number of moles. Moreover, in the simulation units the Boltzmann constant k=1. Hence, the partial pressures

P_i= N_i
V
T,

where N_i is just a number of molecules of certain type.

Your objective is to:

Recognize why the total pressure of the gas mixture is equal to the sum of partial pressures of the components from the microscopic point of view.
You will be able to:
State Dalton's Law.

State the relationship between the number of particles and pressure they exert at constant temperature and volume.

Calculate the final pressure as the number of particles are varied when the initial pressure and number of particles are given.

       N/V             P             T

100 Blue and 100 Green

100 Blue

100 Green

1. Open SMDPlayer, select IntroDalton'sLaw from the IdealGas folder. PRESS Play. Read all the captions and follow the instructions. Go to File -Quit

Movies gives a preliminary understanding of partial pressures from a microscopic point of view.

2. Open SMD, select Dalton in the IdealGas folder.

You are visualizing 100 green particles with a mass of 1.00 and 100 blue particles each with a mass of 10.0 as shown in Figure 2.7.

figures2/pic8c.png

Figure 2.7: Screenshot of Dalton's Law SimuLab.

3. Change the Iterations Between Displays to 500. Select Show Averages.

Increasing Iterations speeds up the simulation.

4. Press Start and run the simulation for approximately 40 time units. Press Pause. Record in your table the number density N/V, pressure P and temperature T from the averaging window.

The system is approaching equilibrium.

5. Select Edit : Edit Particles and choose Remove all G particles. Press Reset Averages in the Average Values panel. Repeat Step 4. Note that the blue particles have a mass of 10.

You are are collecting data for future analysis.

6. Select File : Reset Experiment. Select Edit : Edit Particles and choose Remove all B particles. Repeat Step 4. Note that the green particles have a mass of 1.

7. Using the data recorded in your table, add the pressure of the 100 blue particles to that of the 100 green particles

You are summing partial gas pressures.

Q2.64: Compare this calculated result to the total pressure of the mixture when both blue and green particles were present. Explain what you find.

Q2.65: Does the mass of a particle affect the pressure it exerts? Justify your answer.

Q2.66: What is the relationship between the number of particles present and the pressure they exert in a given container?

8. Select File : Reset Experiment. Select Edit : Edit Particles and choose Remove particles to remove any 20 particles on the screen.

You are lowering the density.

Q2.67: What do you predict the pressure will now be?

9. Select Reset Averages in the Average Values panel. Press Start and wait for 40 time units. Press Pause.

The system is approaching equilibrium.

Q2.68: Verify your pressure prediction.

END ACTIVITY

2.9 Research Projects

Try one of the suggestions below or design your own. Or, feel free to write an essay using any of the questions throughout this chapter as inspiration.

BEGIN ACTIVITY

Research Project 6: Boyle's Law

See SimuLab 7 .

To further investigate the universality of Boyle's law, test it for various temperatures. Set T=1.25, 1.5, 2, 4 and repeat steps 6-8 (in SimuLab 7 for each temperature value.

Q2.69: What happened to the PV product when the temperature increased? Explain.

Q2.70: At low pressures what is the temperature range in which the data is most consistent with Boyle's law?

BEGIN ACTIVITY

Research Project 7: Gay-Lussac Law

See SimuLab 13.

To extend the SimuLab, repeat Step 6 with N/V=0.10.

T=4 T=3 T=2 T=1.25 T=1

Pressure

P/T

Deviation from ave.

% Deviation

Average P/T=

Plot a Pressure vs. Temperature graph. Determine the line of best fit and the slope. Extend the line to P=0. Find the temperature corresponding to P=0.

Q2.71: Contrast this graph to that obtained from the N/V=0.02 experiment. What are the similarities and the differences you see?

Q2.72: What happens to the P/T ratio as the number density of the gas sample is increased? Explain.

BEGIN ACTIVITY

Research Project 8: Charles' Law

See SimuLab 11 .

To see if the Volume vs. Temperature graphs for different pressures are straight lines that cross close to the origin we recommend that you perform the following investigation. Instead of using the prerecorded movie, you should repeat the Charles' Law experiment at different pressures using charles.smd files in the IdealGas folder.

END ACTIVITY

BEGIN ACTIVITY

Research Project 9: Avogadro's Principle

See SimuLab 15 . Open one of the files: Abvogadro40, Avogadro100 or Avogadro200.

Deselect Lock Piston Position check box so that the piston is free to move. Set Pressure to the same value you obtained in the previous experiments. Remove 25 particles by selecting Edit : Edit Particles. Set B particle mass to 5 and predict what will be the volume of the gas at equilibrium. Run the simulation for 1000 time units.

Q2.73: Find the average volume and compare it with your prediction.

END ACTIVITY

BEGIN ACTIVITY

Research Project 10: Ideal Gas Law

See SimuLab 19 .

To more precisely define the temperature and number density range in which the ideal gas law is obeyed, perform 20-40 additional experiments. Using the IdealGas application, run the simulations 20-40 times, changing the temperature and number density parameters as you are measuring the pressure. Draw a Temperature vs. Number Density graph using the data from these experiments. Label each data point with the PV/NT value. The theoretical value of the PV/NT ratio is 1.00. Draw a line connecting the points for which the deviation is less then 5% from the ideal gas value of 1.0. Using your pencils shadow the temperature region for which the ideal gas law is valid.

Q2.74: Describe the region of applicability of the ideal gas law in terms of density and temperature.

END ACTIVITY

BEGIN ACTIVITY

Research Project 11: Gay-Lussac Law II

In order to be confident about the results of an experiment it must be repeated many times. Gay Lussac is remembered for his very precise as well as accurate measurements that he made of T & P as he ascended in a balloon. You can determine the precision (reproducibility) of our measurements. Run the SimuLab for 20 time units, pause the simulation, and record density, pressure, and temperature values for this trial into the first row of the table from SimuLab 13. Calculate the P/T value for this trial and record it into the table. Select Reset Averages in the Average Values panel.

Make a copy of the table below:

Trials N/V P T P/T Deviation from average % deviation

1

2

3

4

5

Average value

Average ( P/T) _avg value:_________;

Do not reset the experiment each time but continue to run the simulation for additional 20 time units from the point it has reached in the previous time interval. Reset Averages after each trial. Repeat the same simulation four (or more) times. Find the average values of density, pressure, and temperature. Determine their deviations from the average value in percents. Find the average value of the P/T ratios and calculate the deviation of each P/T value from the average. Calculate the percent deviation of each ( P/T) _i value from the ( P/T) _avg average ( (|( P/T)_i-( P/T) _avg| )/(( P/T) _avg)×100) ; and calculate the average percent deviation.

Q2.75: What conclusions can you make about the precision (reproducibility) of this virtual experiment?

END ACTIVITY

Chapter 3
Energy and Intermolecular Forces

As we heat a substance, the molecules move faster and faster. Water in contact with melting ice gets colder: the kinetic energy of the water molecules is transferred to the potential energy of those ice molecules that are separating themselves from the ice crystal and moving into the liquid.

3.1 Intermolecular Forces

We learned in Section 1.2 that temperature is proportional to the average kinetic energy of a system:

T � �
� mv²
2
�
� avg
.
(3.1)

where m is particle mass and v is the individual particle velocity. However, this definition is not very enlightening if we do not know the definition of the word " energy.''

So what is energy? The common definition is that energy is the capacity to do work. We know from everyday experience that doing work requires effort, at least for some of us.

When we apply a force to an object and move it in the direction of our applied force, we are doing work¹. For example, we do work when we lift a heavy bag, or shovel snow, or hand-saw wood.

Energy exists in many forms. To say that the energy of an object is the maximum amount of work it can produce is only partially helpful, because different processes enable differing amounts of work. A ten-liter can of gasoline stored on a high shelf is a simple example. If the shelf breaks, and the can falls to the floor, a small amount of work is done and the floor ends up with a scratch. On the other hand, if the gasoline is poured into a car's gas tank and the heavy car is then driven 100 kilometers, a huge amount of work is produced.

Kinetic energy is one form of mechanical energy and is due to the motion of an object (see Section 1.2).

Another form of mechanical energy is potential energy. Potential energy depends on either (i) the position of an object with respect to other objects or (ii) the deformation of an object. In other words, potential energy depends on the geometry of the system.

The most simple example of potential energy is the potential energy due to gravitational force. In mathematical terms, an object of mass m that lies on the edge of an abyss of a depth h has the potential energy

E_P=mgh,
(3.2)
where g � 10m/s² is the free-fall acceleration in the gravitational field of Earth. An object has potential energy if it can perform a certain amount of work in its particular situation.

A rock that is just about to fall off a cliff has potential energy E_p. When the rock starts falling, the gravitational field of the Earth accelerates it so that when it reaches the bottom it has acquired a certain velocity. The potential energy of the rock at the top of the cliff is transformed into the kinetic energy of the accelerating rock, mv²/2. How can we determine this kinetic energy? Due to energy conservation, the total energy of the rock is the same before and after the fall. At the top of the cliff, before the rock falls, it has only potential energy E_P. At the bottom of the cliff it has only kinetic energy E_K. Due to the law of enegy conservation, E_P=E_K.

mgh = mv²
2
.
(3.3)
From this equation we can find the velocity of the ball just before it hits the ground: v=�{2gh}.

Potential energy can be negative depending on where you choose the level zero for the potential energy. If we choose level zero to be at the sea level, then at the bottom of the Dead Sea valley in Israel (404 meters below sea level) the potential energy of a stone weighing one kilogram is 1 kg ×(-404m)× 9.8 m/(sec²) � -4000 Joules. This means that 4000 Joules of work are required to bring the stone up to Mediterranean sea level, where the potential energy is defined to be zero.

Another form of potential energy is the energy stored in a " deformed'' object such as a compressed spring or a drawn bow just before the release of an arrow. When we draw a bow we apply force (and perform work) to pull back the bow-string. This work is stored in the bow in the form of potential energy. When we release the string, it performs work as it rapidly accelerates the arrow forward. The potential energy of the bow is transformed into the kinetic energy of the arrow.

Q3.1: What happen with the kinetic and potential energy of the arrow as the arrow flies up? Clue: The arrow flies in the gravitational field of the Earth

How can the body of the bow store energy? The body stores energy as a result of the internal forces (both attractive and repulsive) between its atoms and molecules. These forces are caused by the electrical charges of the of the bow's molecules and atoms. These forces stores potential energy in the same way as the gravitational force stores potential energy of the rock in the above example. The intermolecular forces between the bow's molecules-molecules that attract and repulse each other-store the energy.

Scientists have discovered that these forces, derived from the intermolecular potential energy, are affected by the distance between the molecules. At very large distances, the forces are so small that essentially the molecules do not interact. As the molecules move closer to each other, the interactions of the nuclei and electrons cause an attraction to develop. When the distance between molecules becomes very small, however, the repulsion between electron clouds of the molecules begin to dominate and the molecules begin to repel each other.

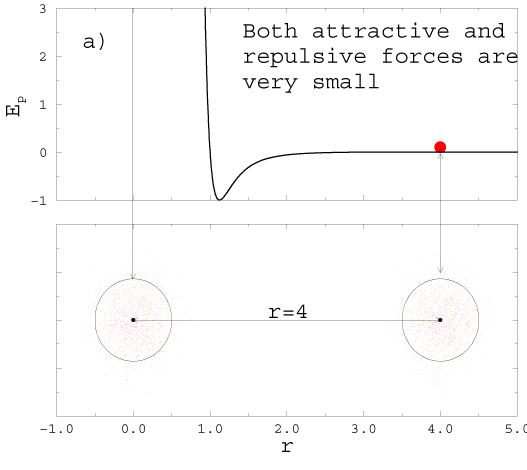
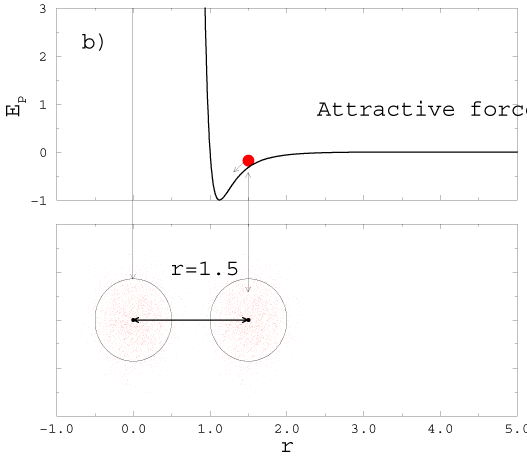
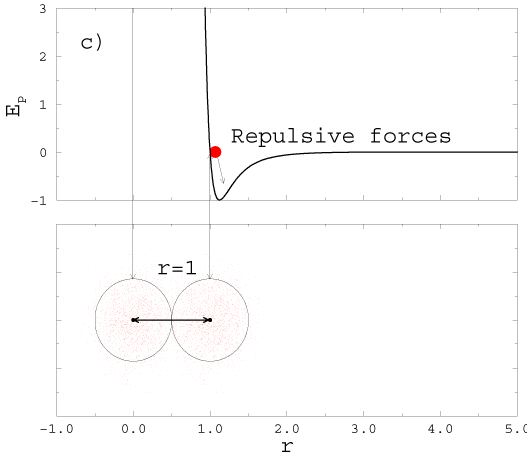
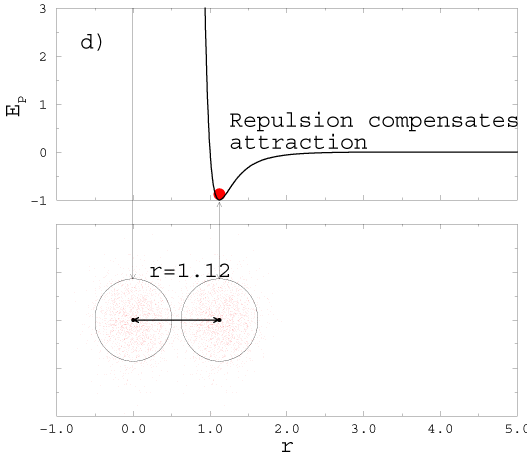
figures1/I.1.1c.gif figures1/I.1.1d.gif

Figure 3.1: Potential energy E_p of intermolecular forces as function of the intermolecular distance r. Each pair of graphs illustrates the interaction of two atoms of noble gases at different distances from each other. The atoms are shown as negatively charged electron clouds with small circles at the center, indicating positively charged nuclei. The two large circles show effective atomic sizes, which correspond to the minimal distance, atoms can approach each other during a collision at low temperature. Above the atoms we show the potential energy landscape of the pair of atoms. The small ball indicates the analogy with the gravitational potential field. The ball in this landscape has the same potential energy as the pair of atoms. The forces acting on the atoms are proportional to the slope of the landscape at the ball's location.

These forces are illustrated in the graph of potential energy E_P versus distance separating molecules r (see Figure 3.1). We treat this graph as a imaginary roller coaster. The height of the graph h determines the potential energy of the pair of molecules in exactly the same way as the height of the ball on the roller coaster determines its potential energy. The steeper the slope of the graph, the larger the attractive or repulsive force.

Note that at the lowest point in the graph, the ball has a negative potential energy of -1, corresponding to a position at the bottom of the " Dead Sea valley''. The flat part of the graph for a very large r corresponds to " Mediterranean Sea level''.

3.1

net

We can also learn from figure 3.1 why substances at different temperatures exist in different states: gaseous, liquid and solid. Recalling that temperature is a measure of the average kinetic energy of molecular and atomic motion, we can conclude that at low temperatures, molecules are trapped in a relatively rigid structure forming a crystal lattice. The molecules position themselves at a distance that minimizes their potential energy, they sit in the " Dead Sea valley's'' of the imaginary potential energy landscape. They have kinetic energies that are much smaller than the potential energy barrier they need to overcome if they are going to escape the relatively rigid solid structure (see figure 3.2).

figures1/epot.png

Figure 3.2: Potential energy of molecule in crystal lattice is at a minimum. Potential barrier must be overcome if molecule is to leave the solid state.

If we put a ball at the lowest point on our imaginary roller coaster and kick it gently, it will move back and forth near this lowest point, but never manage to escape. In the same way, molecules in a crystalline lattice vibrate near their minimal potential energy positions.

As we heat our substance, the molecules move faster and faster. Occasionally some of them acquire a kinetic energy larger than the potential energy barrier and break away. Returning to our roller coaster, if we kick our ball hard enough, it will escape the bottom level of our graph. Its kinetic energy decreases by the amount of potential energy it gains as it climbs up the hill. We know that water in contact with melting ice gets colder: the kinetic energy of the water molecules is transferred to the potential energy of those ice molecules that are separating themselves from the ice crystal and moving into the liquid.

At very high temperatures, all the molecules separate from each other. If we kick our ball very hard, it rolls away from the potential minimum, reaches the plateau part of the graph, and continues to roll forever-or would, were it not for the friction forces that eventually slow it down. In the same way, water molecules leave the surface of boiling water and move away at high velocities in the form of water vapor.

BEGIN ACTIVITY

SimuLab 12: Intermolecular Forces

Your objective is to:

Recognize the forces that acts between particles of gas and relate these forces to the macroscopic behavior of the substance.

You will be able to:
Explore the microscopic interactions of two noble gas atoms.

Study how the forces acting between atoms of noble gases depend on the distance between the two atoms.

Explore the relation between the internal potential energy and the interatomic forces.

Test if the law of conservation of energy is satisfied.

Relate temperature and strength of intermolecular forces to the phase changes.

No. of Distance Particle's Kinetic Potential Total Final

Experiment Behavior Energy Energy Energy State

1 3.5

2 2.0

3 0.9

4 1.2

3.1

Particle's Behavior: Stay in place (A), Attract (B) or Repulse (C)
Kinetic Energy: Stays constant (A), Increases (B) or Decreases (C)

Potential Energy : Stays constant (A), Decreases (B) or Increases (C)

Total Energy : Stays constant (A), Decreases (B) or Increases (C)

Final State : Particles stay apart (A), Oscilate near equlibrium position (B), Move freely in the entire box (C) or Stay close to each other in fixed position (D)

1. Open SMD, select file Intermolecular in the Energy folder.

You see a single particle in the center of the particle screen.

2. Press Start

The particle is completely motionless. Watch the graph of the energies at the right part of the simulation window. It shows kinetic, potential, and total energy of the particle as functions of time by the red, blue, and black lines, respectively. If the red or blue lines are invisible, it means that they exactly coincide with the black line.

3. Press Pause.

The potential energy of a single particle is defined to be zero, because our particle does not interact with any other particles or its surroundings.

Q3.2: What is the kinetic energy of the particle? Explain your answer.

Q3.3: What is the total energy of the system?

4. Reset Experiment from the File menu.

You will be placing another particle at various distances from the existing atom and study their interaction.

5. Select Particles from the Edit menu. The dialog box Edit Particles appears. Select Add Particle G and click mouse inside the particle box near the edge.

A new green particle will appear.

6. Press Start, wait approximately 5 time units and press Pause. Using the graph, record your observations in the table and compare them with your prediction.

Make your observation of the particle behavior and the behavior of the kinetic, potential, and total energies.

7. Reset Experiment from the File menu. Select Particles from the Edit menu. The dialog box Edit Particles appears. Select Add Particle G and place the center of the second particle at the distance of approximately 2 particle diameters from the center of the first one. Repeat Step 6.

8. Reset Experiment from the File menu. Select Particles from the Edit menu. The dialog box Edit Particles appears. Select Add Particle G and place the center of the second particle at the distance of approximately 0.9 particle diameters from the center of the first one. Repeat Step 6.

The edges of the particles should touch each other. Our computer model does not allow particles to be less then 0.8 particle diameters from each other. So try to click the mouse several times, slowly moving the cursor away from the center of the existing particle until you succeed in placing the new particle at the desired distance.

9. Reset Experiment from the File menu. Select Particles from the Edit menu. The dialog box Edit Particles appears. Select Add Particle G and place the center of the second particle at the distance of approximately 1.2 particle diameters from the center of the first one.Repeat Step 6.

There should be a small gap between the edges of the particles.

Q3.4: Explain the observed changes in potential and kinetic energies.

Q3.5: Relate the behavior of the particles to the behavior of the particles in a crystal.

10. Press Pause. Using Temperature scrollbar, increase the value of Temperature to 0.4. Press Start.

You will study the effect of temperature on the particle behavior. The temperature scroll bar indicates the average kinetic energy of the particles at given time. By increasing this value, you are increasing the kinetic energies of both particles by the same amount. The graph of energies indicates the average kinetic energy, average potential energy, and average total energy of each particle. You can precisely determine the values by pressing the mouse at a given position on the graph.

Q3.6: This case corresponds to a crystal melting. Describe the particle behavior in terms of potential energy graph. Clue: See Fig. 3.2.

11. Press Pause. Using the Temperature scrollbar, increase the value of Temperature to 0.5. Press Start.

Predict the particle behavior. Watch the behavior of the particles and determine if your prediction is accurate.

Q3.7: This case corresponds to evaporation. Describe the particle behavior in terms of potential energy graph. Clue: See Fig. 3.2.

END ACTIVITY

3.2 Kinetic and Potential Energy of Particles

BEGIN ACTIVITY

SimuLab 13: Kinetic and Potential Energies of Particles in Gas State

Your objective is to:

Investigate the correlation between the kinetic, potential energies and temperature as gas particles move and collide.

You will be able to:
Define potential energy and kinetic energy and give an example of each.
Discuss the relationship among potential energy, kinetic energy, and total energy before, during, and after a two-particle collision at a given temperature.

State the relationship between the average kinetic energy of randomly moving particles and the temperature of the system.

Describe what happen to the speed of particles in a system as the temperature is raised.

1. Open SMD, select Experiment25 in the Energy folder. Press Start. To speed up the simulations set Iterations between Displays to 5

You are visualizing a low-density gas, see Fig. 3.3. There is no exchange of energy with the surroundings (i.e. the system is thermally isolated). Thus the total energy of the system is conserved. Each gaseous particle moves along a straight line until it collides with another particle or with the container walls.

figures1/SLC01.1.gif

Figure 3.3: You are visualizing 25 green gas particles at temperature T = 1. The temperature T=1 is far above the boiling point of the substance.

Observe the graph Temperature vs. Time (see Fig. 3.3).

The temperature T reading below the screen is an exact computation of the average kinetic energy, E_k of a particle in the system, T = ((mv²)/2 )_avg. The temperature is calculated at every simulation step: the program calculates the kinetic energy mv²/2 for every particle, adds them together and divides by the total number of particles.

Q3.8: Describe the graph and explain why the temperature is not constant?

2. Pause the simulation. Using the scroll-bar, increase the temperature from the current value T=1.0 to a new value T=4.0 and press Start.

Q3.9: Do the molecules move faster or slower? Explain.

3. In order to visualize the change in the kinetic energy of the individual particles, switch the menu Display Particles by to Absolute Kinetic Energies as shown in Fig. 3.4.

Some of the particles are violet, blue, green, yellow and red. The color of each particle indicates the amount of kinetic energy it has as you can see from the Spectrum of Kinetic Energies. The violet particles have the highest kinetic energy (move at the highest speed), then come the blues, then green, then yellow, and then red, which have the lowest kinetic energy (move at the lowest speed). When they collide, their colors change.

Q3.10: What do the changing colors indicate about the particle's kinetic energies as they collide?

figures1/SLC01.2.gif

Figure 3.4: A snapshot of the application screen representing the same gas as in Fig. 3.3, but at temperature 4. The color of each particle indicates its kinetic energy.

4. Switch the menu Display Particles by to Potential energy.

The color coding now indicates the value of each particle's potential energy as you can see in the Spectrum of Potential Energies. Most of the particles are so far away from each other that there is almost no interaction between them. Their potential energy is assigned a value of zero and colored light blue. The particles that are close to each other have a negative potential energy and are colored green.

5. Go to Options - Select Delay and select Short Delay.

You are selecting a short delay to better see the changes of potential energy of colliding particles. When two particles collide, the potential energy increases and the kinetic energy decreases. The total energy of the interaction remains constant. The increase in potential energy of the two particles is indicated by a change of color to dark blue and violet. The decrease in kinetic energy of the two particles is indicated by the dip in temperature on the temperature graph.

6. Switch the Graph to Energies. Turn off the delay.

On the energy graph the average kinetic energy of the particles is indicated by the red line, the average total energy of the particles is indicated by the black line, and the average potential energy of the particles is indicated by the blue line.
The total energy is constant as is reflected in the flatness of the black line (see Fig. 3.5).

Q3.11: Try to explain the peaks in the graph of kinetic and potential energies. Why are they complementary? Clue: Watch if they correspond to the moment of a collision

Q3.12: Why does the total energy of the system-which is the sum of its kinetic and potential energy-remains constant?

figures1/SLC01.3.gif

Figure 3.5: The same system as in Fig. 3.4. The color of each particle now indicates its potential energy. A pair of colliding particles with a positive potential energy appears in bright magenta. The graph showing potential energy vs. time (bottom curve) indicates the maximum at the time of collision (Time � 9.75). The graph showing kinetic energy (top curve) indicates the minimum at that point. The fluctuations of kinetic and potential energies are, in fact, complementary (in the sense that peaks in potential energy correspond to dips in kinetic energy, and vice versa)-and the total energy of the system, indicated by a straight black line, is constant.

END ACTIVITY

BEGIN ACTIVITY

SimuLab 14: Kinetic and Potential Energies of Particles in Liquid State

Your objective is to:

Recognize the difference between a gas and a liquid in terms of the energies of the particles.

You will be able to:
Differentiate among the liquid and gas state in terms of average kinetic energy and the average potential energy of the particles.

Contrast the potential energy of a molecule in the center of a droplet with that on the edge of the droplet.

State the relationship between the trajectory of a particle and its potential energy.

Explain the release of latent heat when a gas condenses.

1. Open SMD, select Experiment 1 in the preset experiments in Energy folder and press Start. Make sure that the Iterations between Displays are 5.

You are visualizing 144 particles of a high-density gas. There is no exchange of energy with the surroundings (the system is thermally isolated) and thus the total energy of the system is conserved.

2. Pause the simulation and reduce the temperature to 0.01. Press Start.

At first the particles almost stop, but then they start to accelerate toward each other, and form little droplets. The formation of droplets is called condensation and occurs naturally in clouds.

Q3.13: Do you expect a particle in the center of a droplet to have the same or different potential energy when compared to a particle at the edge of the droplet. Explain your reasoning.

3. In order to speed up the simulations change Iteration between Displays to 100. Press Pause and switch Display Particles by to Potential Energy and press Start.

The temperature steadily increases until it levels out. Notice that the droplets break apart and that the color of particles in the middle of the droplets changes to yellow (i.e these particles have a relatively low potential energy).

Q3.14: When you lowered the temperature of the system to 0.01 what happened? Explain the rise in temperature you observe.

If you continue the simulation long enough (50-60 unit times), the temperature will rise sufficiently that the particles in the droplets will have enough kinetic energy to break away and travel through the surrounding gas (see Fig. 3.6). The droplets will stop growing and will continually break apart and reform.

figures1/SLC01.4.gif

Figure 3.6: The system showing the gas near its condensation point. Little droplets of liquid form, but almost immediately break apart. The color coding indicates the potential energy. The particles in the droplets are green and yellow, indicating that they have relatively low potential energy.

4. Switch the Graph to Energies. If mor than 50 time units elapsed, Reset the experiment and repeat step 2.

Notice how, during the experiment, the average potential energy decreases while the average kinetic energy has increased.

Q3.15: Explain why during condensation, in a thermally isolated system, many small droplets form, but they do not coalesce to form a single dropplet.

figures1/SLC01.5.gif

Figure 3.7: The system is at constant temperature of T=0.4. The graph shows average kinetic energy (top line), total energy (middle line), and potential energy (bottom line), all with virtually no fluctuation. Almost all the gas condenses into liquid droplets that are in equilibrium with the surrounding gas, which is of extremely low density. Some of the particles escape from the droplets and some coalesce with them. The color coding indicates the potential energy of each particle. Note that the particles in the middle of the droplet have the lowest potential energy. The time on the graph indicates the time elapsed since the beginning of condensation, i.e., since the temperature was lowered from T=1 to T=0.4.

5. Reset the experiment. Switch Display Particles by to Potential Energy. Switch the Graph to Energies and set the temperature to 0.4. This temperature is below the condensation point. Put the Heat Bath on and press Start. Watch the system for 200 times units.

In order to simulate a gas-liquid transition, we must cool the system further. In order to achieve this, the latent heat of condensation that is produced must be dissipated into the larger surrounding system. This is done on the computer by putting the Heat Bath on. Now the system will exchange energy with the surroundings. See how the droplets form steadily.

Q3.16: What happens to the energies, E_k, E_p and E_T of the system?

6. Because the condensation process requires a significant amount of computer time, we recommend opening the Experiment1a file. Switch the graph to potential energies.

This starts the experiment at the stage where almost all the particles have coalesced into large droplets (see Fig. 3.7).

Q3.17: Watch the colors of the particles in the big droplet (see Fig. 3.7). In the center they turn to orange and yellow while on the edges they remain green.

Explain why? Clue: how many neighbors do the particles in the center have compared to those on the edge?

Q3.18: Explain the changes you see in terms of potential energy of particles at the moment when a particle leaves the droplet and when it joins the droplet.

7. Switch Display Particles by to Trajectories and press Start.

The particles in the droplet move along curved lines, while in the gas they move along straight lines.

Q3.19: How do you explain these trajectories in terms of the potential energies of the particles?

END ACTIVITY

BEGIN ACTIVITY

SimuLab 15: Sublimation, Deposition, and Triple Point.

Your objective is to:

Recognize sublimation, deposition and triple point from a microscopic point of view.

You will be able to:
Describe the process of deposition and explain it in terms of potential energy.

Describe the process of sublimation and explain it in terms of energy.

Compare and explain the potential energies of particles that exist at the triple point.

Describe molecular motion at the triple point.

1. Open SMD, select Experiment 1a in the Energy folder, set Iterations between Displays to 500 and press Start.

The experiment starts at the stage where almost all the particles have coalesced into large droplets. The Heat Bath is on. You see 144 particles in contact with a thermal bath whose temperature is T=0.4.

2. Switch Display Particles by to Potential Energy. Pause the simulation. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears type in: " Liquid'' and press Ok.

3. Now drop the temperature to T=0.3.

This temperature is below the freezing temperature of the substance.

4. Press Start.
After 100 time units, pause the simulation.

Watch the changes in the colour representing the potential energy of the particles.
The particles in the gas start to form little " snowflakes'' that eventually merge with the large crystal. This phenomenon is called deposition.

Q3.20: What happens to the droplet?

5. Select Take a Snapshot - Screen. When the dialog box with the Title of the Picture appears type in: " Solid'' and press Ok.

Q3.21: Now compare the snapshots in the two phases. What differences do you see? Explain.

Q3.22: What happens to the potential energy of the system when you drop the temperature to 0.3?

figures1/SLC01.6.gif

Figure 3.8: The system at temperature T=0.3. The droplet is frozen into a " triangular'' crystal. The time on the graph indicates the time elapsed since the beginning of crystallization, i.e., since the temperature was lowered from T=0.4 to T=0.3. Next to the crystal is a little " snowflake'' that will eventually coalesce with the crystal. The few gaseous particles are in equilibrium with the crystal.

Q3.23: Are there any particles not in the solid state? If yes describe them.

6. Deposition requires a significant amount of computer time to simulate. We recommend opening the Experiment1b file in order to skip the earlier stages of the process and press Start. Switch Display Particles by to Potential Energies .

You see some gas molecules surrounding the crystal. The gas has much lower density than before. The gas particles separate from and rejoin the crystal. This happens to snow in very cold weather-it gradually disappears, moving directly from the crystalline snowflake state into the water vapor state without ever passing through the liquid water state. The same thing happens to solid carbon dioxide (CO₂, " dry ice'') when it turn into a gas. This phenomenon is called sublimation.

7. Set the temperature to T=0.33 which is the temperature of the triple point. At this temperature all three phases-solid, liquid, and gas-coexist. Press Start.

Q3.24: What happens to the crystal?

8. Switch Display Particles by to Trajectories in order to see the movement of particles in the three states of matter.

Q3.25: Watching the trajectories of the particles identify the three states of matter. How can you distinguish gas, liquid and solid in terms of the particle trajectories?

9. Set temperature to T=0.4. Watch the changes in the crystal. Set temperature to T=1.0. Describe the changes in the system.
10. Switch Display Particles by to Absolute Kinetic Energy. Watch the color of the particles.

Q3.26: Do all the particles move at the same speed? Explain what you see.

END ACTIVITY

Appendix A
Answer Key

Temperature and States of Matter

Q1.1 The three states of matter are solid liquid and gas.

Q1.2: All three have the same molecular formula and molecular structure, H₂O.

Q1.3: They differ primarily in their inter-molecular structure and the amount of energy which these molecules possess. Molecules in ice possess the least amount of energy, are located in the same position over time, and possess only vibratory motion. Liquid water molecules are in constant contact, but have no definite structure; they possess translational motion within the volume of the sample. Gaseous water molecules are in constant random motion within their container, have no intermolecular bonding structures, and possess the most energy of the three types (at a given temperature).

Q1.4: The speed of the translational motion decreases as more and more molecules begin to aggregate. Finally, the molecules are found in a definite pattern, and possess only vibratory motion.

Q1.5: While the molecules remain in constant contact,the speed of their translational motion increases; at the surface interface molecules would leave the liquid, and would possess the individual random translational motion characteristic of a gas.

Q1.6: The answer may vary. The answer should be in draw or in words that the molecules are closer in solid that in liquid and closer in liquid than in gas.

Q1.7: When we heat a solid the motion of particles changes because molecules move faster. In terms of the structure if we heat a solid above the condensation point it became a liquid or a gas, so the geometric array is lost.

Q1.8: If we decreases the temperature of a gas, the molecules start to move slowly. If the temperature is decrease below a certain point the gas condenses or even freeze (See Q1.10).

Q1.9: The answer is (b).

Q1.10: The molecules will move slower and form a crystal arrangement again.

Q1.11: Trajectories of liquid particles tend to be curved lines; for particles in the solid phase the trajectories are very limited-one may see some back-and-forth motion. The trajectories reflect the amount of intermolecular forces which are at work.

Q1.12: The answers may vary, one example is water vapor in the air at the dew point.

Q1.13: The answer is (c). Trajectories of gaseous particles are straight lines; those of liquid particles tend to be curved lines. The trajectories reflect the amount of intermolecular forces which are at work. Very little force exists among gaseous molecules. More force exists among molecules in the liquid phase, such that translational motion is limited to the volume of the liquid.

Q1.14: The answer is (c).

Q1.15: Trajectories of gaseous particles are straight lines; those of liquid particles tend to be curved lines; for particles in the solid phase the trajectories are very limited-one may see some back-and-forth motion. The trajectories reflect the amount of intermolecular forces which are at work. Very little attractive force exists among gaseous molecules, this fact produces straight trajectories. More attractive force exists among molecules in the liquid phase, so this liquid particles have translational motion but limited to the volume of the liquid.

Q1.16: For a given substance at a given atmospheric pressure, the state of matter is directly related to the temperature, with the solid phase having the lowest temperature and the gaseous phase the highest. As the temperature is raised , beginning from the solid state, the particle tends to move faster, and thus begins to overcome the intermolecular forces which hold it in place within the solid. At the lowest temperature it experiences vibration only, but as the temperature rises it experiences translational motion, first within the liquid which has formed as the crystal lattice breaks up, and subsequently the straight line motion characteristic of the gas phase. See Q1.15.

Q1.17: Students answers will vary. The answer is: departing from the solid phase, the liquid is a greater temperature than the solid and the gas is a greater temperature than the liquid and the solid. See Q1.15.

Q1.18: As the temperature is raised the trajectory become curve and finally is a straight line.

Q1.19: Students answers will vary. At the center and the edge the trajectory at T=0.1 indicates a solid. At T=0.4 the center particle usually has a liquid (i.e curved) trajectory. The edge particle at T=0.4 may exhibit trajectories of either a liquid or a gas. At T=2 both go to gas phase (straight lines trajectories).

Q1.20: The ranking is (c), (b) and (a). In case (b) the kinetic energy will be two times larger than in case (a) and in case (c) it will be four times larger.

Q1.21: The answer is 3.5

Q1.22: The answer is �{11}

Q1.23: The average speed of particles increases and so does the average kinetic energy. The explanation is that the average kinetic energy is proportional to the temperature and does so the average of the squared speed.

Q1.24: Heavier particles move slower than lighter particles. Let M be the mass of the heavier particles and m is the mass of the lighter. Let the average square velocity of the heavier particle be V and the square velocity of the lighter particle be v. At equal temperature the average kinetic energies of heavy and light particles are equal: (M V²)/2 = (m v²)/2 thus V=v ×�{ m/M}. The coefficient �{ m/M} is less than one. Hence the V < v.

Q1.25: The average velocity will increase by a factor of 10. As the average kinetic energy is proportional to temperature, the average kinetic energy will increases by a factor of 100 and because the mass does not change the average square velocity will increases by a factor of 100 thus the velocity increases by a factor of 10.

Q1.26: The pattern of the spreading of food coloring is very complex. In part it can be explained by the convective motion in water. In simple words, the pattern is created by particle of water bumping onto particles of food coloring. The average kinetic energy of particles in hot water is greater that the average kinetic energy of particles in cold water and thus the particles of food coloring move faster in hot water.

Q1.27: The temperature is 4.

Q1.28: The average kinetic energy is also 4 because in our simulation temperature is equal to the average kinetic energy.

Q1.29: Yes it does, see previous question.

Q1.30: No it does not, because the selected particles frequently collides with other particles and change its velocity and, hence, its kinetic energy also changes.

Q1.31: The velocities of the particles are different because particles collide in different way and the velocities change after each collision. Each time they collide they interchange kinetic energy and thus the colors change.

Q1.32: As more and more velocity updates are taken into account the histogram become smooth due to general laws of probability and statistics.

Q1.33: The velocity at the maximum of the histogram is 2. This velocity will be equal to 0.5 at T = 0.25 and equal to 1 at T=1 since this velocity v_max = �{ T/m} is proportional to the square root of the temperature. Note that this v_max is not the same as the average velocity plotted in the histogram. The average kinetic energy is equal to the temperature so 1/2 m (v²)_avg and (v)_avg �{ 2 T/m}.

Q1.34: The position of the maxima of the velocity distributions should coincide, within the measurement error , with the predictions. If you find any discrepancy, increase the number of observations.

Q1.35: At different temperatures, the distributions are similar in shapes and are different in the position of the maximum (See Q1.33 and Q1.36) , the width and the height.

Q1.36: The colors of the particles' screen refers to the individual kinetic energies. At higher temperatures the histogram is wider because the average kinetic energy is bigger, that means that the range of kinetic energies of individual particles is greater at high temperatures that at low temperatures. As the velocities are proportional to the square root of the kinetic energies its distribution spread at high temperatures with respect to the case at low temperatures.

Q1.37: The velocity at the maximum of the histogram is 0.5 for m=4 and 3.1 for m=0.1 since this velocity is proportional to the square root of two times the temperature divided by the mass (in two dimension is equivalent): v_max=�{ T/m}.

Q1.38: At different masses the distributions have similar shapes. However, the position of the maximum (see Q1.37), the height of this maximum and the width of the distribution changes. As the mass is increased, the height of the maximum increases by a factor of �{ m/M} where M is the initial mass and m is the final mass, and the height changes by the inverse factor so the total area of the histogram remains the same (100 %).

Q1.39: The positions of the maximum velocity values should coincide, within the error in the observation, with you predictions.

Q1.40: The colors are the same because at fixed temperature the kinetic energies are the same, but the velocity distribution depends on the mass.

Q1.41: The value of the temperature is 1 and the value of the mass is 1 for both particles. Thus the velocity distribution will coincide.

Q1.42: The velocity distributions, for B and G particles, for the initial settings are similar because they have the same mass and the same average kinetic energies. When we change the B particle mass the histogram of particle B changes (see Q1.38) while the distribution for particles G remains the same. When density is changed the velocity distribution does not change. When we increase the temperature to 4 the maximum of the velocity distribution shift by a factor of 2 for both types of particles. The width spreads by a factor of 2 and the height changes by the inverse factor so the total area of the histogram remains the same (100 %).

Q1.43: The shape of the crystal and the colors of the particles (indicating kinetic energy) for different masses are the same. When you increase the density the gas becomes fluid and the crystal changes it shape due to the large pressure exerted by the fluid. The colors of the particles (indicating kinetic energy) are the same as at low density. When we increase temperature to 4 the crystal melts and as the range of kinetic energies increase, the colors of many particles change to green, blue, and violet.

Q1.44: According to the molecular kinetic theory, the shape of the distributions of the velocities should be always the same. The width should depend only on temperature and mass. If you find something different, it may mean that the system during your measurements is not at thermal equilibrium. Note: The number of velocity distribution observation should be always larger than 10000. If the density of the system is very small, this number should be even larger, because at small densities, the particles collide very rarely and do not exchange their kinetic energies.

Q1.45: The system will behave according to the parameter changes, you have made. In general, at low temperatures the system will condense into or crystallize. It will also crystallize under high pressure.

Q1.46: At the beginning, all the particles have the same speed, assigned by the computer program. Thus at the beginning the distribution of particle velocities is a narrow tower located at the average velocity corresponding to the average kinetic energy. This situation can never happen in nature, because as particles collide, their velocities change according to the law of energy conservation. In some collisions very fast and very slow particles may appear. After many collisions, the distribution spreads and acquires its unique stable shape, predicted by the British scientist J. C. Maxwell (1819-1867).

Q1.47: On the graph, you see the average kinetic energy of B particles (blue line), G particles (green line) and the average kinetic energy of all the particles (black line). The black line is always in between the blue and the green lines because it is an average of both kinetic energies. At the beginning the average kinetic energy of blue particles is much smaller than that of the green particles. As the time goes on the system reaches thermal equilibrium because the fast particles of the gas collide with slow particles of the crystal and transfer their kinetic energy to the crystal.

Q1.48: The velocity distribution of green particles shrinks and the velocity distribution of blue particles spreads, so at equilibrium they are equal.

Ideal Gases

Q2.1: Yes. Your thumb prevents air from escaping, the descending piston reduces the gas volume, therefore there are more collisions per unit time with the wall. This causes the internal pressure to increase and this is the resistance you feel.

Q2.2: The handle comes back up. Initially the internal pressure of the gas is greater than the external pressure and thus the gas pushes the piston (i.e. handle) up.

Q2.3: Yes. You are applying force on the coil and the coils pushes back. By pushing you are disturbing the coil from its equilibrium position.

Q2.4: Yes. You increase the volume of the gas as you pull the piston back. The pressure inside decreases and the pressure outside remains constant. This difference is responsible for the resistance you feel.

Q2.5: You feel a resistance to stretching because the coil is being moved from it's equilibrium position.

Q2.6: If the area of your palm is 50 times the area of your finger, the pressure on your palm would be 50 times smaller.

Q2.7: The force is the weight of the book. The book has a mass of 1 kilogram which is equivalent to the weight of approximately 10 Newtons (=1 kg × 10 m/(s²)). The pressure on your palm is Force/Area = 10N/(1.5 ×10^-2 m²) � 670 Pascals. The pressure on your finger is 10N/(3×10^-4m²) � 33,000 Pascals!

Q2.8: As the water vapor condenses, there will be almost no gas left inside (i.e. very small internal pressure). The relatively large atmospheric pressure which presses on the outside of the bottle crushes the bottle.

Q2.9:Student answers may vary; the number will be around seven collisions.

Q2.10: The pressure will fluctuate a little; there are relatively few particles and therefore the collisions with the piston from each will be more noticeable than if there are many particles, as in a real gas sample.

Q2.11: The piston will move downward on the screen. The reverse will be true if the internal pressure is greater than the external.

Q2.12: It will be equal to the external pressure. For the system to be at equilibrium implies that the forces on the piston caused by the two pressures have become equal.

Q2.13: The piston will vibrate slightly up and down around a fixed position.

Q2.14: In a real gas at equilibrium the volume will remain constant over time. In our simulation the volume will vary about 5% over time, due to the fact that there are relatively few particles, and the pressure changes caused by each colliding with the piston will result in small but noticeable changes in the pressure (see answer to Q2.10).

Q2.15: The relatively small number of particles causes small, though noticeable variations in volume (see the volume vs time graph).

Q2.16: The gas at equilibrium will have pressure, volume and temperature values which are constant.

Q2.17: The average volume should be reduced by a factor of two.

Q2.18: The piston descends because the external pressure (0.08) is greater than the internal pressure (which is initially 0.04). The volume is reduced by one half. (to approximately 2200)

Q2.19: Answer depends on students' observations. Students should find the program is consistent to Boyle's law within �0.03.

Q2.20: There are approximately twice as many segments on the second graph. This is due to the fact that the particles collide with the piston on average twice as often as when the external pressure was 0.04.

Q2.21: As the volume decreases the frequency of collisions increases by the same factor.

Q2.22: As frequency of collisions increases the gas pressure increases by the same factor.

Q2.23: There are relatively few particles in the sample, thus the pressure change caused by each particle colliding with the piston registers as a noticeable change on the graph.

Q2.24: There is no appreciable change in the fluctuations.

Quantitative Boyle's Law Table (Values may vary).

1,000 2,000 4,000 8,000 10,000

Temperature 1.25 1.249 1.25 1.25 1.25

NumberDensity 0.2 0.1 0.05 0.025 0.02

Volume 1,000 2,000 4,000 8,000 10,000

Pressure 0.26 0.125 0.063 0.031 0.025

PV 260 250 252 248 251

Dev. from Average 7.8 2.2 0.2 4.2 1.2

% Deviation 3.25% 0.872% 0.079% 1.66% 0.476%

Average PV value: 252.2

Average % Deviation:1.267%

Q2.25: The average percent deviation is approximately 1.3%. There is good agreement between the calculated results and those one would expect to obtain, based on Boyle's Law.

Q2.26: The graph is not a perfect hyperbola because it is based on only 200 particles.

Q2.27: The slope of the graph is the average PV product (i.e slope is P/( 1/V)=PV). The P vs. V graph gives a hyperbola, the P vs. 1/V graph is linear.

Q2.28: The relationship between P and Number Density is a direct proportion. Both graphs are linear.

Q2.29: The slope is approximately 1.2. The slope corresponds to the gas temperature (which is 1.25 in this case).

Q2.30: You expect a slope of zero (horizontal line). At low pressures (less than .15) the PV product varies within 1%. The PV product increases as temperature increases.

Q2.31: The temperature is in between the other two bowls, but the sensations one feels are misleading. The hand from the hot water registers the water as cold; the hand from the cold water registers the same water as hot.

Temperature Height

1 .099 65

2 .079 35

3 .049 15

Q2.32: The plug of liquid rises.

Q2.33: Warm the sample to a higher temperature (e.g. immerse it in hot water) or cool it to a lower temperature (e.g. immerse it in ice water). Mark your straw every 0.5 inch as before.

Q2.35: The higher the temperature the greater the height of the gas sample. The higher the temperature the faster the gas molecules move and the gas volume expands.

Charles' Law Movie Table (Values may vary).

T₁ T₂ T₃ T₄ T₅

Temp. 1.995 1.803 1.6 1.399 1.19

Pressure 0.0497 0.05 0.0495 0.05 0.049

# Density 0.0246 0.0275 0.031 0.036 0.042

Volume 8212 7420 6543 5673 4808

V/T 4116.3 4115.4 4089.4 4055 4040

Dev from ave 114.43 113.53 87.53 53.13 39

% Dev. 2.86% 2.84% 2.19% 1.33% 0.97%

Average V/T � 4001.87

Average percent deviation=2.9%

Q2.35: The data should give a linear graph, passing through the origin 0,0.

Q2.36: The volume of the gas is directly proportional to the temperature.

Q2.37: The students' graph when they extrapolate the line on the V vs. T graph will come very close to the origin; this temperature corresponds to

absolute zero.

Q2.38: The V/T values generally increase as the temperature increases. The average percent deviation should be about 3%.

Q2.39: Students should obtain an hyperbola.

Q2.40: Number density and temperature are indirectly related; as temperature increases, number density decreases,

Gay-Lussac Table (Data may vary)

T=4 T=3 T=2 T=1.25 T=1

Pressure 0.082 0.061 0.040 0.025 0.020

P/T 0.021 0.020 0.020 0.020 0.020

Deviation from average 0.001 0.00 0.00 0.00 0.00

% deviation 4.950% 0.00% 0.00% 0.00% 0.00%

Average ( P/T) _ave value: 0.0202

Average % deviation=0.990

Q2.41: Typical results shown in the table above.

Q2.42: P/T constant is very precise. There is very little or no variation in the value.

Q2.43: The graph will be linear. Extrapolating the line to P = 0 should give a value of T = 0 (representing absolute zero).

Q2.44: The temperature is zero when P=0 implying that the molecules cannot be moving (i.e. no collisions means no pressure).

Avogadro's Principle Table (Values may vary).

T P V N (# of particles) mass

Avogadro40 1.5 0.03 2,000 40 1.0

Avogadro200 1.5 0.03 10,000 200 1.0

Avogadro100 1.5 0.03 5,000 100 1.0

Avogadro100 1.5 0.03 5,000 100 10.0

Q2.45: Volume changes.

Q2.46: There is a direct relationship between the number of particles and volume. The number of particles increased by a factor of 5 as did the volume. Note that the pressure fluctuations became smaller as the number of particles increased.

Q2.47: Volume becomes 5000. In going from 200 to 100 particles the number of particles has been halved so the volume will also have been halved.

Q2.48:The parameters of temperature, pressure, and number density volume should remain unchanged. Mass density should increase.

Q2.49: Temperature, pressure, and volume remained unchanged as mass of particles was increased.

Q2.50: The number density remains unchanged.

Q2.51: Mass density increased ten times. Number density depends on number of particles and volume (both parameters remain unchanged), while mass density depends on mass of particles and volume. While the volume has not changed, the mass of particles has increased; thus the density has increased.

Q2.52: The volume would be 100 particles/5000= 175 particles/x;x= 500×175/100=8750

Q2.53: Their pressures and number densities will be the same. The mass density of neon will be five times that of helium.

Q2.54: The total number of particles is halved.

Q2.55: Volume will be halved. The initial volume is 2473; the final volume is 1215.

Q2.56: The mass density, ( mass/volume), has increased because the volume has decreased.

Q2.57: The number density remains unchanged because both the number of particles and the volume changed by the same factor (halved).

Q2.58: Avogadro's principle states that at the same temperature, pressure, equal volumes of gases haven equal number of particles. When the number of particles is halved (2 atoms combined to form 1 molecule of product) the volume was also halved since the pressure and temperature remained constant.

Q2.59:Run the SimuLabs and record values of pressure, volume, temperature and number of particles; determine if PV/NT is a constant value.If it is, the gas is ideal.

Ideal Gas Law Table (Values may vary).

Temp Pressure Volume N N/V PV/NT

A 1.25 0.025 10,000 200 0.02 1.003

B 1.3 0.0129 10,000 100 0.01 0.992

C 0.996 0.0195 10,000 100 0.01 0.979

D 1.0 0.0978 2,007 200 0.1 0.981

E 1.0 0.185 1,000 200 0.2 0.925

F 1.0 0.650 422 200 0.5 1.37

G 0.5 0.009 10,000 200 0.02 0.932

H 2.0 0.040 10,000 200 0.02 1.01

I 4.0 0.081 10,000 200 0.02 1.02

The bolded values, are within 5% of the ideal value of 1.0.

Q2.60: (1.003+0.992+0.979)/3=.991 Student values will vary but will be close to 1.0.

Q2.61: The ratio is very close to 1.0. At this density the gas still behaves like an ideal gas.

Q2.62: As the density of the gas increases the gas behaves less and less like an ideal gas. In other words, the ratio deviates more and more from the expected value of 1.0.

Q2.63: The ratio is most consistent at the higher temperature of two and four. At the lower temperature of 0.5 the ratio deviates more than 5% from the expected value.

Dalton's Law Table

N/V P T

100 Blue+100 Green 0.08 0.10 1.25

100 Blue 0.04 0.0467 1.2

100 Green 0.04 0.05 1.25

Q2.64: The calculated result is obtained by adding the partial pressures from the table: 0.0467+.05=0.0967. The total pressure recorded in step 4 is 0.10. Values will vary slightly. These values are approximately the same because partial pressures can be added to get the total pressure.

Q2.65: The mass of a particle does not affect pressure. When the mass of the particle was increased by a factor of 10 the pressure remained unchanged.

Q2.66: The number of particles is directly proportional to the pressure (e.g. if the number of particles is doubled, the pressure is doubled).

Q2.67: P=.01. By removing 20 particles from the original number of 100 we have reduced the number 5 times and thus the pressure decreased 5 times.

Q2.68: The pressure determined by the program should be in very close agreement with that predicted in the previous answer.

Energy and Intermolecular Forces

Q3.1: Kinetic energy decreases as the arrow flies up. When it stops going up, its kinetic energy has fallen to zero, and its potential energy has reached its maximum, which is equal to the initial kinetic energy according to the law of conservation of energy.

Intermolecular Forces Table

No. of Distance Particle's Kinetic Potential Total Final

Experiment Behavior Energy Energy Energy State

1 3.5 A A A A A

2 2.0 B B B A B

3 0.9 C B B A C

4 1.2 A A A A D

Q3.2: Kinetic energy is equal to zero because the velocity of the atom is equal to zero.

Q3.3: It is also equal to zero because it is the sum of potential and kinetic energies.

Q3.4: When the two particles collides the potential energy increases and the kinetic energy decreases according to the law of conservation of the energy.

Q3.5: The behavior of particles in a crystal corresponds to the case where the particle distances are such that they oscillate around a fixed position (around 1.2 particle diameters apart).

Q3.6: At this temperature, particles would move more freely and can leave the crystal. In terms of potential energy, this would correspond to large oscillations in the graph. Particles that have enough kinetic energy to overcome the barrier enter the gaseous phase.

Q3.7: At this temperature, all particles move freely. All particles have enough kinetic energy to overcome the barrier and enter the gaseous phase.

Q3.8: The graph oscillates around a horizontal line which represents an average value of the temperature. The oscillations are due to the fact that our sample contains only 25 particles, thus the average will not be the same for each computer time interval; a larger number of particles would give averages which varied less from the given temperature.

Q3.9: They move faster. Consistent with the equation defining kinetic energy, (mv²)/2 , since the mass, m, remains constant, the velocity, v must increase if the temperature is increased.

Q3.10: The changing colors indicate that the kinetic energies of the colliding particles do not remain constant, but rather are changed during the collisions.

Q3.11: The ''peak'' in one graph (e.g. kinetic energy) always corresponds to a ''valley'' in the other graph (e.g. potential energy). They correspond because, as the particles collide, the total energy will be conserved (as can be seen on the black line). Thus when two particles collide, their kinetic energies will decrease, while their potential energies will increase. Similarly, when they separate, the potential energies will decrease (since work is being done on the two particles) and the kinetic energies will increase (as a result of work having been done on them).

Q3.12: Since the system is thermally isolated (heat is neither added or removed), and energy is a conserved quantity, the total energy of the system is constant. Thus the sum of the potential and kinetic energies must remain the same.

Q3.13: Students answer may vary. Correct answers will include the fact that a particle in the center of the droplet has more neighboring particles than an edge particle and therefore a lower potential energy is expected.

Q3.14: The particles began to coalesce into small droplets. In this process, potential energy is transformed into kinetic energy (latent heat of vaporization) and the temperature rises accordingly.

Q3.15: As no heat can be released from the system and the potential energy decreases during condensation the kinetic energy increases. This allows the particles to leave a given droplet and avoids the formation of one big droplet.

Q3.16: The kinetic energy remains essentially constant (which would be expected when the heat bath is on). Both the potential and total energies decrease by the same amounts; as the potential energy (from the latent heat of condensation) is converted into kinetic energy, this energy is then dissipated into the heat bath, leaving the total energy reduced in the system.

Q3.17: Particles in the center have several nearest neighbors. These interactions lower the potential energy of the particles (see Fig. 3.1d)). Particles on the edges have fewer nearest neighbors and thus less interactions and thus higher potential energy.

Q3.18: A particle leaving the droplet enters the gas phase in which the potential energy among particles is negligible, thus it will assume a blue color. A gaseous particle joining the droplet has experienced an attractive force, and thus has experienced a reduction in potential energy (see Figure 3.1b).

Q3.19: Gas particles do not feel intermolecular forces between each other, so they travel in straight lines until they collide. Liquid do feel intermolecular forces between each other, so they travel in curved lines.

Q3.20: The droplet becomes more ''compact''and then solidifies.

Q3.21: There is a noticeable increase in order among the particles in the solid compared to the liquid.

Q3.22: It has decreased from the initial reading (e.g., -1.42 to -1.85).

Q3.23: Few particles are still in the gaseous phase, as is indicated by their blue color.

Q3.24: The edges become less regular, and there is a noticeable breakdown in the order of the particles near the edges.

Q3.25: The phases can be distinguished by their trajectories. Gaseous particles travel in straight lines while those which have liquified travel in curved paths, still within the aggregate, but near the edges. Solid particles vibrate about fixed positions which can be identified near the center of the aggregate.

Q3.26: The particles do not all move at the same speed, as is evidenced by their different colors on the absolute kinetic energy spectrum. As they collide, they exchange energies, in which case some slow down, some speed up.

Appendix B
Simple Molecular Dynamics: A Quick Reference

Appendix C
Laboratory Materials

4. Real Gases

Using Universal

Simulab 1. Size of a Molecule

Simulab 2. Molecules' Interaction Parameter

5. Molecular Motion

Using SMD program

HandsOn 1. Diffusion Chamber.

HandsOn 2. Tea bags.

HandsOn 3. Golf ball, water and salt.

HandsOn 4. Brownian Motion.

HandsOn 5. Melting in open air, water, and on frying pan.

Simulab 1. Effusion of Gases. Grahams Law.

Simulab 2. Diffusion in Gases. Grahams Law

Simulab 3. Diffusion and Convection.

Simulab 4. Distribution of molecular velocities.

Simulab 6. Brownian motion.

Simulab 7. Barometric formula.

Simulab 8. Heat transfer in gases, liquids, and solids.

Simulab 9. Diffusion in gases, liquids, and solids.

6. Thermochemistry

Using SMD program

SimuLab 1. Heat, work, and internal energy.

SimuLab 2. Heat capacity at constant volume and constant pressure.

Simulab 3. Enthalpy conservation.

Simulab 4. Endothermic and Exothermic reactions. Enthalpy of formation.

7. Phase transitions

Using SMD

SimuLab 1. Vapor Pressure, Enthalpy of vaporization.

Simulab 2. Melting Point.

Simulab 3. Boiling Point.

Simulab 4. Triple Point.

Simulab 5. Critical Point.

Simulab 8. Phase Diagram.

8. Liquids and Solids

Using Universal program

Simulab 1. Hooke's law.

Simulab 2. Thermal expansion.

Simulab 3. Heat capacity of solids and liquids.

Simulab 4. Ionic solids.

Simulab 5. Metallic solids.

Simulab 6. Metastable states.

Simulab 7. Glass formation.

Simulab 8. Why water expands upon cooling.

Simulab 9. Allotropes.

10. Solutions

Using Universal program

Simulab 1. Solvation.

Simulab 2. Energy of Solvation.

Simulab 4. Decomposition of supersaturated solution.

Simulab 5. Phase Diagram of Solution. Solubility Limit.

Simulab 6. Henry's law.

Simulab 7. Rault's Law.

Simulab 8. Boiling point elevation and freezing point depression.

Simulab 9. Osmotic pressure.

11. Water

Using Water program

HandsOn 1. Freezing of a glass bottle of water.

HandsOn 2. Measuring water volume as function of temperature.

HandsOn 3. Solvation of salts.

SimuLab 1. Two water molecules forming a hydrogen bond.

Simulab 2. Structure of ice and its melting (qualitative)

Simulab 3. Evaporation of water. (qualitative)

Simulab 4. Expansion of water upon cooling.

Simulab 5. Ice melting (quantitative)

Simulab 6. Boiling point (quantitative)

Simulab 7. Vapor pressure (quantitative)

Simulab 8. Hydration shell around an ion.

Simulab 9. Why salt melts ice?

Simulab 10. Solvation of salts.

Simulab 11. Why noble gases have much poorer solubility than salts.

12. Macromolecules

HandsOn 1. Epoxy glue

HandsOn 2. Guch-Joule Effect.

HandsOn 3. Egg Membrane.

HandsOn 4. Soap films.

HandsOn 5. Gelation.

Simulab 1. Dance of a macromolecule. Is it alive or dead?

Simulab 2. Polymerization.

Simulab 3. Oil refinery.

Simulab 4. Elasticity. Why rubber shrinks upon heating?

Simulab 5. Micelle Formation.

Simulab 6. How Soap Works.

Simulab 7. Solution of macromolecules.

Simulab 8. Gelation.

Simulab 10. Membranes, Osmosis.

Simulab 11. Colloids.

Simulab 12. Protein folding.

Simulab 13. Molecular motors.

Simulab 14. DNA replication.

12. Chemical Kinetics.

Simulab 1. Rate Laws.

Simulab 2. Activation energy.

Simulab 3. Catalysis.

Simulab 4. Chemical Equilibrium.

Simulab 5. Equilibrium Constant.

Simulab 6. Le Chatelier's Principle.

Footnotes:

¹Energy and work are measured using the same unit, the Joule. One Joule equals the amount of work performed when one Newton of force moves an object one meter. Approximately one Joule of energy is required to lift a stick of butter (100g) from the floor to the table (a distance of about 1 meter).

File translated from T_EX by T_TH, version 3.13.
On 21 Oct 2002, 15:09.

Volume	1000	2000	4000	8000	10,000
Temperature
Number Density
Pressure
PV
Deviation from average
% deviation

	T	P	V	N (# of particles)	mass
Avogadro40
Avogadro200
Avogadro100
Avogadro100

	T=4	T=3	T=2	T=1.25	T=1
Pressure
P/T
Deviation from ave.
% Deviation

Trials	N/V	P	T	P/T	Deviation from average	% deviation
1
2
3
4
5
Average value

No. of	Distance	Particle's	Kinetic	Potential	Total	Final
Experiment		Behavior	Energy	Energy	Energy	State
1	3.5
2	2.0
3	0.9
4	1.2

	1,000	2,000	4,000	8,000	10,000
Temperature	1.25	1.249	1.25	1.25	1.25
NumberDensity	0.2	0.1	0.05	0.025	0.02
Volume	1,000	2,000	4,000	8,000	10,000
Pressure	0.26	0.125	0.063	0.031	0.025
PV	260	250	252	248	251
Dev. from Average	7.8	2.2	0.2	4.2	1.2
% Deviation	3.25%	0.872%	0.079%	1.66%	0.476%

	T=4	T=3	T=2	T=1.25	T=1
Pressure	0.082	0.061	0.040	0.025	0.020
P/T	0.021	0.020	0.020	0.020	0.020
Deviation from average	0.001	0.00	0.00	0.00	0.00
% deviation	4.950%	0.00%	0.00%	0.00%	0.00%

	Temp	Pressure	Volume	N	N/V	PV/NT
A	1.25	0.025	10,000	200	0.02	1.003
B	1.3	0.0129	10,000	100	0.01	0.992
C	0.996	0.0195	10,000	100	0.01	0.979
D	1.0	0.0978	2,007	200	0.1	0.981
E	1.0	0.185	1,000	200	0.2	0.925
F	1.0	0.650	422	200	0.5	1.37
G	0.5	0.009	10,000	200	0.02	0.932
H	2.0	0.040	10,000	200	0.02	1.01
I	4.0	0.081	10,000	200	0.02	1.02

	N/V	P	T
100 Blue+100 Green	0.08	0.10	1.25
100 Blue	0.04	0.0467	1.2
100 Green	0.04	0.05	1.25

Contents

Overview

Simple Molecular Dynamics Feature Tour

Chapter 1 Temperature and States of Matter

1.1 States of Matter

SimuLab 1: Temperature and the State of Matter

1.2 Temperature

HandsOn 1: Observing Particle Motion in Hot and Cold Water

SimuLab 2: Velocity Distribution

1.3 Research Projects

Research Project 1: States of Matter

Research Project 2: Velocity Distribution

Research Project 3: Velocity Distribution II

Research Project 4: Velocity Distribution III

Research Project 5: Velocity Distribution IV

Chapter 2 Ideal Gases

2.1 The Concept of Pressure

HandsOn 2: Tire Pump and Coil Spring

HandsOn 3: Atmospheric Pressure

2.2 Boyle's Law

SimuLab 3: Qualitative Investigation of Boyle's Law

SimuLab 4: Quantitative Investigation of Boyle's Law

2.3 Temperature

HandsOn 4: The Subjective Sensation of Temperature

HandsOn 5: HandsOn: Galileo's Thermometer

SimuLab 5: Galileo's Thermometer - Movie

2.4 Charles Law

SimuLab 6: Charles' Law - Movie

2.5 Gay-Lussac Law

SimuLab 7: Gay-Lussac Law

2.6 Avogadro's Law

SimuLab 8: Avogadro's Principle

SimuLab 9: Avogadro's Principle Movie

2.7 Ideal Gas Law

SimuLab 10: Ideal Gas Law

Consequences of the Ideal Gas Law

2.8 Dalton's Law

SimuLab 11: Dalton's Law

2.9 Research Projects

Research Project 6: Boyle's Law

Research Project 7: Gay-Lussac Law

Research Project 8: Charles' Law

Research Project 9: Avogadro's Principle

Research Project 10: Ideal Gas Law

Research Project 11: Gay-Lussac Law II

Chapter 3 Energy and Intermolecular Forces

3.1 Intermolecular Forces

SimuLab 12: Intermolecular Forces

3.2 Kinetic and Potential Energy of Particles

SimuLab 13: Kinetic and Potential Energies of Particles in Gas State

SimuLab 14: Kinetic and Potential Energies of Particles in Liquid State

SimuLab 15: Sublimation, Deposition, and Triple Point.

Appendix A Answer Key

Temperature and States of Matter

Ideal Gases

Energy and Intermolecular Forces

Appendix B Simple Molecular Dynamics: A Quick Reference

Appendix C Laboratory Materials

4. Real Gases

5. Molecular Motion

6. Thermochemistry

7. Phase transitions

8. Liquids and Solids

10. Solutions

11. Water

12. Macromolecules

12. Chemical Kinetics.

Footnotes:

Chapter 1
Temperature and States of Matter

Chapter 2
Ideal Gases

Chapter 3
Energy and Intermolecular Forces

Appendix A
Answer Key

Appendix B
Simple Molecular Dynamics: A Quick Reference

Appendix C
Laboratory Materials