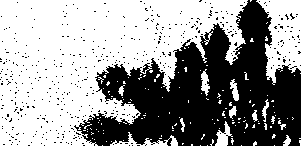
We wanted to find out how the fractal dimension of dendritic lead crystals grown by single replacement reaction in a silica gel containing dissolved lead nitrate would depend on the activity of the reducing metal. Our hypothesis was that the greater the potential difference between lead and the reducing metal, the more rapidly the pattern would develop, and the lower the fractal dimension in accord with earlier results showing that the fractal dimension of metallic crystals growing in the ECD system was lower with the higher growth rate in the higher salt concentration.
List of Materials:
Petri dishes
Lead nitrate
Sodium silicate
Graduated cylinders
Magnesium ribbon
Small piece of copper and zinc sheet
Paper clip (stainless steel)
Glacial acetic acid
Balance
Syringes
Parafilm
Beakers
Stirring rods
Preparation of Lead Nitrate Gel
A sodium silicate gel containing lead nitrate was prepared in a manner modified from that in Appendix G of Patterns in Science, 1996. For each Petri dish, the amount of sodium silicate solution described in step #1 of the procedure was doubled. In the second step, 0.15 g of lead nitrate was dissolved in the acetic acid solution. This final solution was also needed in double the amount specified in the manual. (Note: Too little dissolved lead will result in a reaction that is too slow for the dendritic pattern to develop in a reasonable time; to much lead will result in the formation of a white precipitate when the two gel components are mixed.) The two components were then poured into the bottom of a Petri dish and stirred. The dishes were covered and sealed with Parafilm and allowed to gel overnight.
Growth of Lead Crystals
Surfaces of small strips of copper, magnesium, and zinc (2 to 4 mm in width, and 6 to 8 mm in length) and a similar length of paper clip (mainly iron) were cleaned. The metal strips were positioned in the center of the lead-containing gels with their long dimension oriented vertically. The strips were pushed through the gel and touched the bottom of the dish. The lids were once again placed on the Petri dishes and the dishes sealed with Parafilm. The lead crystals were then allowed to grow.
Method of Analysis
All Petri dishes were periodically examined for growth of lead crystals. The extent of radial growth after 20 and 40 minutes was recorded. The crystals were later examined under magnification and two representative sites captured to computer by means of a Sony CCD micro video camera. Resulting images were then opened into NIH Image and saved as MacPaint files. These images were later opened into Fractal Dimension and fractal dimensions determined using the edge method. Other images were acquired by using a flatbed scanner to scan the bottom of each Petri dish. Crystal images were saved as MacPaint files and further analyzed using Fractal Dimension as described above.
No dendrites formed in the system employing copper as the metal. Branching crystals formed in all the other dishes. The growth was evident within minutes, as was the rate of growth. After the crystals had grown overnight, the extent of branching in the system containing iron was about 5 mm. Growth in the system with zinc reached a little over 1 cm, while using magnesium as the reducing metal resulted in some dendrites about 3 cm long.
Sample crystal images captured under magnification are shown below. The limited branching in the iron system, and the extensive dendrites in the magnesium system can be seen.
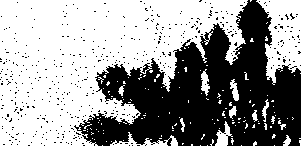
Figure 1. Lead crystal formed with iron as reducing metal.

Figure 2. Lead crystal formed with zinc as reducing metal.

Figure 3. Lead crystal formed with magnesium as reducing metal.
Scanned images for iron were unsatisfactory because the entire crystal covered less than 2 cm2. The image for zinc was marginal. Only the magnesium crystal was large enough to yield a scanned image from which the fractal dimension could be obtained with some confidence.
Preparing images of the magnified crystals for analysis using Fractional Dimension was painstaking. Although the crystal structure was very clear to the naked eye, the cloudiness of the gel coupled with the uneven reflection of light led to digital images of less than ideal contrast. The images were eventually processed to an extent that was satisfactory for working with Fractional Dimension. Because of the way in which portions of the image were selected for analysis, it was clear that the perimeter method would be the most satisfactory for data analysis. The outlined perimeters did show good resemblance to the edges observed with the naked eye and under magnification. The table below shows the potential difference between each of the reducing metals and the lead ion along with the value of the fractional dimension of the resulting lead crystal. The potential differences were determined from data in a table of oxidizing potentials. Magnesium exhibited a much larger potential difference than either zinc or iron, and resulted in a substantially higher fractal dimension.
| Reducing Metal | Potential Difference (Volts) | Fractal Dimension |
|---|---|---|
| Iron | 0.314 | 1.40 |
| Zinc | 0.637 | 1.43 |
| Magnesium | 2.240 | 1.50 |
The data above was entered into Graphical Analysis. Graph 1 below suggests a linear relation between potential difference and fractional dimension.
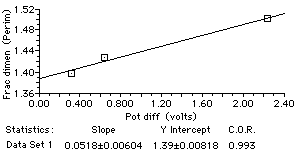
Graph 1. Fractional dimension vs. Potential Difference
As hypothesized, no crystal growth resulted when a piece of copper was placed in the center of a Petri dish containing lead nitrate dispersed in a silica gel. We anticipated that this would be the case, since copper falls below lead in tables of relative activity of metals. Also as hypothesized, growth of elemental lead crystals was much more rapid when magnesium was used as the reducing metal than it was when zinc or iron were used. Magnesium exhibits one of the highest oxidation potentials of all metals. Iron, which lies closest to lead in oxidation potential, showed dendritic growth, but the growth rate was very slow. Again, this was expected because the difference in oxidation potentials drives the single replacement reaction.
We could clearly see differences in the structure of the lead crystals grown under the different conditions. We easily noted such differences even viewing with the naked eye and under a hand-held magnifying glass. The crystals in the iron system showed the least distinctive branching. Dendrites were more extensive in the zinc system; there was more branching than with iron, but still considerable filling in. Magnesium's oxidation potential was much farther removed from that of lead than were the other two metals. The resulting crystal structure was remarkably different. The growth might be described as more spindly, with more frequent and thinner branches. Unlike the other two systems, the sub-branches were very often at right angles to the branch from which they developed. The appearance suggested that these crystals would show the greatest fractal dimension.
Graph 1 shows a linear relation with positive slope between fractal dimension of a lead crystal and the potential difference between the reducing metal and lead. Contrary to our hypothesis, the fractal dimension in this case was greatest where the growth rate was greatest. This was opposite the result in ECD systems where the variable was the solution strength; in that case, more rapid growth was reported to lead to a lower dimension. This pair of results demonstrates that the growth rate itself does not determine the fractal dimension. We are confident of the trend in our data in that it corresponded to our visual sense of the crystals. We are far less confident of the actual numbers for fractional dimension. The limitations of the method of analysis lead to considerable uncertainty, as do the limited numbers of measurements for each crystal. The high correlation coefficient on the graph should be regarded with some skepticism because of the high likelihood of a good fit to three points, two of which are quite close in the value of the independent variable.