
HandsOn 14 - Building an Aggregate by Hand
Figure shows a large random aggregation pattern. This pattern was grown using the random walk you are about to use. Your job is to start a random walker on the rim of the surrounding circle. Then let the walker stagger around the grid until it reaches the black pattern. When the walker reaches the black pattern, it sticks and becomes a black square. Then another walker starts from a random point on the rim of the surrounding circle and staggers around until it sticks to the pattern. And so forth. That's all there is to our model. This model is called diffusion-limited aggregation, or DLA for short and comes from the fact that the growth rate of the pattern depends on the rate at which particles arrive at the surface by diffusion (the net motion due to their random walk).
 |
Figure
4.8: An aggregation resulting from a random-walk model. This pattern
was built from a single "seed'' (black square with white
dot) by releasing 170 random walkers, one at a time, from the
rim of the surrounding circle and allowing each to walk until
it reaches and sticks to the growing pattern.
|
2. Choose a starting place for the walker on the rim of the circle by spinning
your pencil like a propeller as you drop it onto the figure. Place your walker
wherever the tip of the pencil points on the rim of the circle.
3. Now roll a 4-sided die and move your walker one space right, left, up,
or down. (You can also use a six-sided die; when you get a 5 or a 6, do not
move the walker, just roll again. Some game stores sell tetrahedral, 4-sided,
dice.)
There is one exception to the rule above: If the next move takes the walker
outside the circle, remove the walker and start a new one from another random
location on the rim. This eliminates walkers that wander away from the pattern.
4. Repeat rolling the die and moving the walker until your walker lands next
to a filled square of the pattern: right, left, above, or below the filled
square (not a diagonal position). When this happens, fill in the square
the walker is sitting on. That is the new addition to the aggregation.
It may take quite a while to add one more square to the aggregation. You spend
a lot of time rolling and reading the die. To shorten this time, we have programmed
a computer to "roll the die'' and print out a table, Figure . In this
table L and R mean "left'' and "right," respectively, while U and D mean
"up'' and "down.'' To read the table, start anywhere you want and
read in a straight line horizontally or vertically, without repeating any
line.
5. Spin the pencil again to point to a new starting point on the circle. This
time one of you read out loud the letters from Figure ("up,'' "right,''
"up,'' "down,'' etc.) while the other one moves the walker. How
fast can you make your moves using the new method? Remember, whenever a walker
moves outside the circle, remove it and start a new walker.
6. When the walker lands next to a black square of the aggregation (to the
right, left, above, or below), fill in the square and start again.
7. Continue this process until you have added about 10 squares to the aggregation.
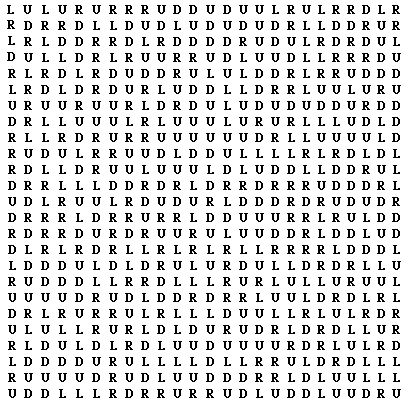 |
Figure
4.9: Randomly-generated table of steps up, down, left, and right
(U, D, L, R). Read a line of letters from the table to direct
your 2-D walker.
|
|
|
Previous: 4.3 - Modeling Fractal Growth