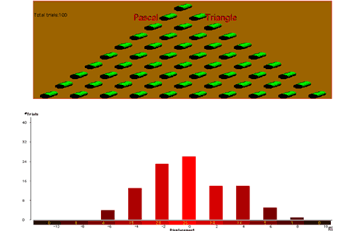
3.4 - Pascal's Triangle

SimuLabs:

5. Random Walk and Pascal's Triangle

6. Width of a Distribution

7. Average Position after N steps

In the preceding section we found that some predictability grows out of random coin flipping, leading to a "bell-shaped'' bar graph of the results. Such a distribution is also called the normal or Gaussian distribution (you will encounter this distribution at many places in this site). This section carries the idea further, relating random coin flipping to random motion. Random movement is important for understanding the microscopic world in nature, because atoms and molecules move randomly. How can we describe the random motion of molecules in, say, a gas? Molecules are too small to see, so to help us think concretely we replace a molecule with something we can see: a wandering ant. If a wandering ant starts at a lamp post and takes steps of equal length along the street, how far will it be from the lamp post after a certain number, say N, steps? Though this question is seemingly trivial, it poses one of the most basic problems in statistical science.