HandsOn 7 - Circle Measurement of Dimension
One method we have
been using to measure fractal dimension is the method of covering. There
are other methods for measuring dimension. One that is useful for objects with
dimension less than or equal to two involves measuring the total area of the
object present inside circles of different radii. For a surface in a plane,
the area increases as the square of the radius: A = ![]() R2. The power
2 of R tells us-again!-that a disk is 2-dimensional.
R2. The power
2 of R tells us-again!-that a disk is 2-dimensional.
Check results
of the formula A = ![]() R2 by counting the
number of cells inside circles of different radii in the Figure. For each circle,
count all the cells inside that circle, not just those between that circle and
the next smaller circle. Enter your results in a copy of Table 2.5.
R2 by counting the
number of cells inside circles of different radii in the Figure. For each circle,
count all the cells inside that circle, not just those between that circle and
the next smaller circle. Enter your results in a copy of Table 2.5.
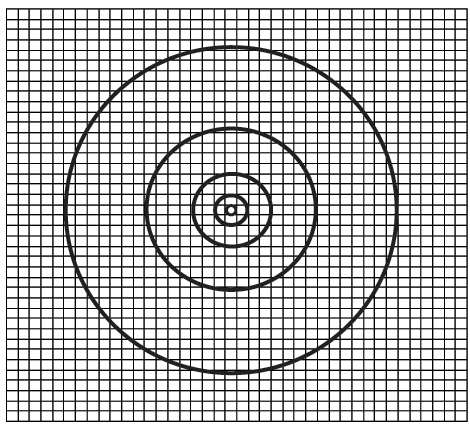 |
| r (radius) | N (count) |
| 0.5 | |
| 1.5 | |
| 3.5 | |
| 7.5 | |
| 15.5 |
Plot the results from your copy of Table 2.5 on a log-log graph, the radius scale along the horizontal axis and N along the vertical axis. From the measurement of the slope, calculate the dimension of the circular surface in Figure 2.7.
Now measure the dimension of the line in Figure using a similar procedure. First, count the number N of short line segments inside each circle of radius r. Enter the results in a copy of Table 2.8. Second, plot N versus r on a log-log graph and measure the slope. What is the value of the dimension of the line?
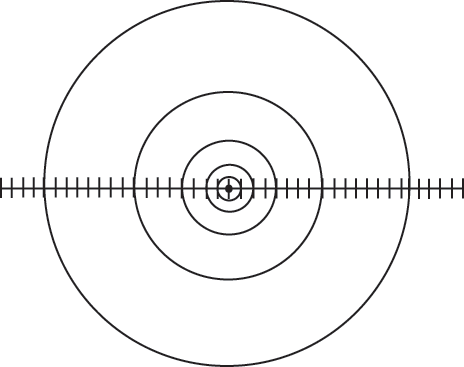 |
| r (radius) | N (count) |
| 1 | |
| 2 | |
| 4 | |
| 8 | |
| 16 |
|
|
Previous: HandsOn 6 - 1-, 2-, & 3-Dimensions