Activity 1: ``Walking'' Along a Coastline

Stepping Along a Coastline with a Caliper

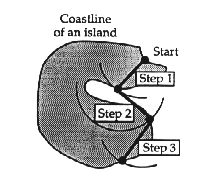
To investigate coastlines, start by ``walking'' along the map of a coastline (see Figure 1).

• 1. Obtain the following:
  • [A.] a map of the coastline to be measured.
  • [B.] a pair of calipers (dividers). A caliper or divider is like a circle-drawing compass, except that both ends have points.
  • [C.] this table.

    1. Size of step, S	2. Predicted Number of Steps, N	3. Measured Number of Steps, N	4. "Length"= N*S

• [2.] Make decisions about:
  • [A.] the points on the map between which to measure the length of coastline
  • [B.] the scaled distance on the map for the first setting between the ends of the calipers (preferably a multiple of two, such as 64 kilometers or 32 miles).
• [3.] Separate the points of the calipers by the scaled distance of step 2B. Place the first end of the calipers at the beginning of the coastline to be measured and swing your calipers so that the second end rests on the coastline as close to the starting point as possible. This is step number 1.
• [4.] Now swing the caliper so that the first end ``walks'' along to the nearest next point on the coastline. This is step number 2.
• [5.] Continue this process, counting the steps as you go; stop when your next step would carry you beyond the end of the coastline. The total number of steps multiplied by the distance covered in each step gives an initial measurement of the length of your coastline. For example: 10 steps, each of a scaled length of 64 kilometers, yields a total length of 10 * 64 kilometers = 640 kilometers.
• [6.] Enter the size of the step (in miles, kilometers, or whatever) in the left column of your copy of Table 1 (above). Enter the number of steps in the third column.
• [7.] Now you are going to start again, this time reducing the distance between the calipers to half its original value. Before you do this, predict the number of steps it will take you to walk along the coastline with this smaller step size. Enter your prediction in the second column of your copy of the table.
• [8.] ``Walk'' along the coastline with the calipers set to half the original distance. This is equivalent to a child (instead of an adult) walking a shoreline. Count the total number of steps and record the results in the correct columns of your copy of Table 1. How accurate was your predicted number of steps?
• [9.] Repeat the process of cutting in half the distance between the caliper points as many times as you can, each time making a prediction, taking the walk, and filling in your copy of the table with your results.
• [10.] Fill in the right-hand column of your copy of the table by multiplying each step size by the number of steps to get a total ``length.''

Did your prediction of the number of steps become more accurate with each new setting of the calipers? What happens to the total length of the coastline for different step sizes? Take a guess: What is the ``final length'' of the coastline as the step size gets smaller and smaller?

Now you are going to plot on graph paper the data you collected from your coastline measurements.

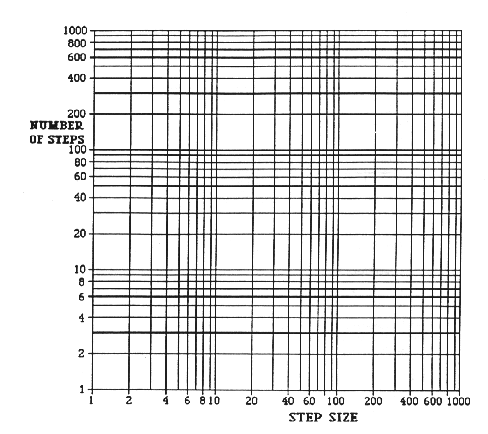
This is a special kind of graph paper. If you have not used such graph paper before, the uneven scales may appear odd.

These scales, called logarithmic or ``doubling'' scales. Basically, the numbers 1, 2, 4, 8, 16, ... occur at equal intervals along each axis, as do the numbers 1, 10, 100, 1000, ... When logarithmic scales are along both axes, the graph paper is called log-log paper. For now, you need to know only one thing about this novel scale: You can add a zero to all the numbers along either axis and the graph paper is equally useful. For example, the vertical axis can be relabeled 10, 20, 40, ..., or 100, 200, 400, ... or 0.1, 0.2, 0.4, ... If the entries in your copy of the table do not match the numbers on one axis of the graph paper, just multiply all the numbers on that axis by 10 or by 1/10 until they do match.

1.

Plot the numbers from your table on a copy of the graph paper. Plot the number of steps along the vertical axis and the step size along the horizontal axis. What kind of curve do the plotted points form? Do they lie along a straight line? When they lie along a straight line on this kind of graph, it is possible to define the object's dimension. The dimension is equal to the magnitude of the slope of this straight line. For some objects this slope---this dimension---is not a whole number. Objects with non-integer dimension are called fractals (meaning they have ``fractional'' dimensions).

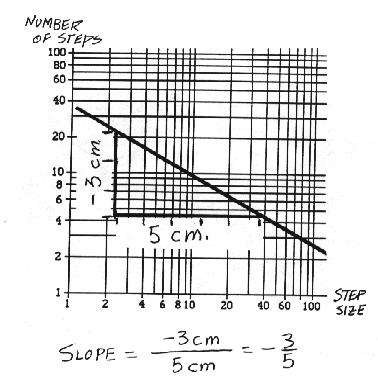
2.

With a ruler, draw by eye the ``best'' straight line using the points on your graph. Determine the magnitude of the slope of your graph. The slope is defined as the change in vertical rise along the line divided by the change in horizontal run along the line (or "rise" over "run").

These vertical and horizontal changes are laid out using linear measures, not logarithmic. Use a regular ruler to measure this slope, not the scale along the axes. What is the magnitude of the slope (the dimension) of your coastline?

d	Number of Segments of length d needed to span line of length L=100	Number of squares of side d needed to cover square of area L2=10000	Number of cubes of edge d needed to fill cube of volume L3=106
1
2
5
10
20
50
100