We run computer simulation programs to predict and study the properties of a system in bulk. For the present we are not interested in surface effects. But our simulations track only a small number of particles in order not to slow down the computation. As a result, most molecules are near the edge of the sample, that is near its ``surface.'' Therefore, it looks like we cannot avoid surface effects in our computations. The system size would have to be extremely large to ensure that the surface has only a small influence on the bulk properties, but this system would be too large to simulate. A glass of water, for example, has a very large system size in comparison to its surface. In contrast, water in a drinking straw has a much smaller system size compared with its surface.
To eliminate surface effect from the computation we use a trick. Surface effects can be ignored for all system sizes if we use periodic boundary conditions. In periodic boundary conditions, the cubical simulation box is replicated throughout space to form an infinite lattice. In the course of the simulation, when a molecule moves in the central box, its periodic image in every one of the other boxes moves with exactly the same orientation in exactly the same way. Thus, as a molecule leaves the central box, one of its images will enter through the opposite face. There are no walls at the boundary of the central box, and the system has no surface. The central box simply forms a convenient coordinate system for measuring locations of the N molecules.
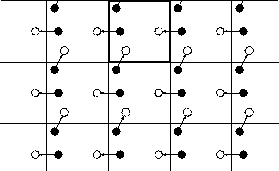
A two--dimensional version of such a periodic system is shown in Figure 3.3.1. As a particle moves through a boundary, all its corresponding images move across their corresponding boundaries. The number of particles in the central box (and hence in the entire system) is conserved.

Fig. 3.3.1 Periodic boundary conditions. The central box is outlined by a thicker line.
It is not necessary to store the coordinates of all images in a simulation (this would be an infinite number), just those of the molecules in the central box. When a molecule leaves the box by crossing a boundary, attention may be switched to the identical molecule just entering from the opposite side.
It is sometimes useful to picture the single central simulation box in our two dimensional example as being rolled up to form the surface of a three dimensional torus or donut (Fig. 3.3.2 -- 3.3.5). Think of drawing two perpendicular dashed lines across the middle of a piece of typing paper parallel to its edges (Fig. 3.3.2.) Now roll up the paper so that two sides meet to form a hose with circular ends (Fig. 3.3.3 and 3.3.4.) Next bend the hose until the two circular ends meet. The results is a torus or donut (Fig. 3.3.5.) Each original dashed line now closes on itself. A particle following either one of these lines comes back to the same point on the donut, just as a particle in the central box of the infinite lattice in Figure 3.3.1 comes back to the same location if it follows a straight line.

Fig. 3.3.2 The unit cell as a rectangular piece of paper. Dashed lines show trajectories of two particles traversing the unit cell.

Fig. 3.3.3 Beginning to curl the unit cell into a tube.
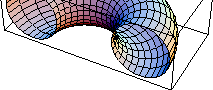
Fig. 3.3.4 The unit cell as a tube.

Fig. 3.3.5 Connecting the ends of the unit cell as a tube to form a donut. Particles traversing the dashed lines in the original unit cell (Fig. 3.3.2) will return to the same location on the donut. (Dashed lines are not shown in this figure.)
With the donut configuration there is no need to consider an infinite number of replicas of the system, nor any image particles. The donut correctly represents the topology of the two--dimensional system, if not the geometry. A similar analogy exists for a three--dimensional periodic system, but this is more difficult to visualize.